Bonjour! :)
Pouvez-vous m'indiquer sur quelle piste je dois partir pour résoudre ce problème?
Soit X et Y deux variables indépendantes de loi N(0,1).
Montrer que X+Y est indépendante de X-Y.
Merci à vous ;)
[L2] Lois normales centrées réduites / Indépendance
5 messages
- Page 1 sur 1
par Nightmare » 18 Jan 2013, 16:04
Salut,
une piste : Etudie la densité de probabilité du couple (X+Y,X-Y) en effectuant un changement de variable adéquat.
une piste : Etudie la densité de probabilité du couple (X+Y,X-Y) en effectuant un changement de variable adéquat.
par Deluxor » 18 Jan 2013, 17:14
Bonsoir Nightmare!
Merci pour ton indication. Je ne maîtrise pas bien le changement de variable. Voici ce que j'ai tenté :
Déjà, on a : \, = \, \frac{1}{sqrt{2\Pi}} \, e^{-\frac{x^2}{2}})
et  \, = \, \frac{1}{sqrt{2\Pi}} \, e^{-\frac{y^2}{2}})
Ainsi, comme X et Y sont indépendantes : \, = \, \frac{1}{2\Pi} \, e^{-\frac{x^2+y^2}{2}})
.
On pose :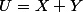
et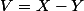 
) \, = \, \iint_{\mathbb{R}^2} \, h(x+y,x-y) \, f_{X,Y}(x,y) \, dx dy)
) \, = \, \frac{1}{2\Pi} \, \iint_{\mathbb{R}^2} \, h(x+y,x-y) \, e^{-\frac{x^2+y^2}{2}} \, dx dy)
On pose
Alors :
On a donc montré que \, \mapsto \, (x+y, x-y))
est bijective et que =(\frac{u+v}{2},\frac{u-v}{2}))
On a de plus : ) = \frac{-1}{2})
Donc :) \, = \, \frac{1}{4\Pi} \, \iint_{\mathbb{R}^2} \, h(u,v) \, e^{-\frac{(\frac{u+v}{2})^2+(\frac{u-v}{2})^2}{2}} \, du dv)
Je doûte avoir compris la méthode...?
Merci pour ton indication. Je ne maîtrise pas bien le changement de variable. Voici ce que j'ai tenté :
Déjà, on a :
Ainsi, comme X et Y sont indépendantes :
On pose :
On pose
Alors :
On a donc montré que
On a de plus :
Donc :
Je doûte avoir compris la méthode...?
par lionel52 » 20 Jan 2013, 15:52
Sinon X+Y est une loi gaussienne, de même que X-Y.
Si tu calcules la covariance Cov(X+Y,X-Y) = Var(X)-Var(Y) ça te donne 0 et pour des lois gaussiennes A et B, Cov(A,B) = 0 équivaut à A et B indép. donc X+Y et X-Y sont indépendantes
Si tu calcules la covariance Cov(X+Y,X-Y) = Var(X)-Var(Y) ça te donne 0 et pour des lois gaussiennes A et B, Cov(A,B) = 0 équivaut à A et B indép. donc X+Y et X-Y sont indépendantes
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :