Lois marginales !!

[sniperamine]

Bonsoir tout le monde voilà je vous expose mon problème :
soit D l'ensemble suivant D={(x,y)E R² , 0<x<=y)} et soit f la fonction définie par f(x,y)=exp(-y)1D(x,y)
1) montrer que f(x,y) est une densité de probabilité
2) détemriner les lois marginales de X et de Y . Sont elles indépendantes
3) X et X-Y sont elles indépendantes ?
4) X et X/Y sont elles indépendantes ?
voilà j'ai tout fait sauf pour la 3éme et la 4éme question j'ai déterminé la loi X-Y et X/Y en utilisant le jacobien etc
so j'aimerais bien savoir s'il n'ya pas une autre méthode ? si oui me la montrer et merci d'avance !!

[sniperamine]

personne ? hmmmmm

[sniperamine]

alors toujours personne ?

[Ben314]

Bonsoir,
Sauf erreur, pour montrer que les deux loies et 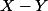sont indépendantes, il suffit de montrer que et, comme les pavés "engendrent" les boréliens, on peut se contenter du cas où et sont des intervalles.

On doit pouvoir le faire soit directement (en calculant les 3 proba. et vu que tu as calculé les loies de X et X-Y, tu doit pouvoir tout calculer assez simplement)

On doit aussi pouvoir l'écrire "de façon théorique" en gardant le "f" dans les trois intégrales et en disant que, pour que la formule soit vraie pour tout il faut regarder les dérivées en , en , en et en de la formule. On devrait trouver une condition sur la fonction f pour que ça marche...

N'étant pas trop sûr que la deuxième méthode aboutisse, je te conseillerais la méthode plus bourrin N° 1...

[sniperamine]

Bonsoir,
Sauf erreur, pour montrer que les deux loies et sont indépendantes, il suffit de montrer que et, comme les pavés "engendrent" les boréliens, on peut se contenter du cas où et sont des intervalles.

On doit pouvoir le faire soit directement (en calculant les 3 proba. et vu que tu as calculé les loies de X et X-Y, tu doit pouvoir tout calculer assez simplement)

On doit aussi pouvoir l'écrire "de façon théorique" en gardant le "f" dans les trois intégrales et en disant que, pour que la formule soit vraie pour tout il faut regarder les dérivées en , en , en et en de la formule. On devrait trouver une condition sur la fonction f pour que ça marche...

N'étant pas trop sûr que la deuxième méthode aboutisse, je te conseillerais la méthode plus bourrin N° 1...

bonsoir ben et merci pour ta réponse justement la première méthode est un peu "bourrine" j'aime pas les calculs lol donc voilà la question est tjrs ouverte et merci bcp d'avoir pris le temps de me répondre

[alavacommejetepousse]

bonjour

il suffit de déterminer la fonction de répartition du couple (X,X-Y) et de passer à la limite pour avoir les fonctions de répartitions marginales et de regarder si la fonction de répartition du couple est le produit des deux

(il y a forcément du calcul dans un exercice de ce genre)

[sniperamine]

bonjour

il suffit de déterminer la fonction de répartition du couple (X,X-Y) et de passer à la limite pour avoir les fonctions de répartitions marginales et de regarder si la fonction de répartition du couple est le produit des deux

(il y a forcément du calcul dans un exercice de ce genre)

bonjour tu peux stp me la calculer ? merci d'avance !!

[sniperamine]

peut on calculer la variance de X et si elle est différente de 0 alors les lois ne sont pas indépendantes ?

[Ben314]

peut on calculer la variance de X et si elle est différente de 0 alors les lois ne sont pas indépendantes ?

Je vois pas trop le rapport entre la variance de X (qui, comme son nom semble le suggérer ne dépend que de ... X) et le fait que X et Y sont indépendantes.

Par contre si tu parle de la covariance de X et Y, ben... c'est un peu à ça que ca sert la covariance : à voir si c'est ca dépend l'un de l'autre...

[sniperamine]

Je vois pas trop le rapport entre la variance de X (qui, comme son nom semble le suggérer ne dépend que de ... X) et le fait que X et Y sont indépendantes.

Par contre si tu parle de la covariance de X et Y, ben... c'est un peu à ça que ca sert la covariance : à voir si c'est ca dépend l'un de l'autre...

bonsoir ben tout à fait d'accord avec toi par contre j'ai remarqué que si V(X)=0
E(X²)=E(X)² donc E(X)E(Y)-E(X²)=E(X)E(Y)-E(X)² ça implique que
E(X(Y-X))=E(X)(E(Y)-E(X)) ( car X et Y sont indépendantes )
donc on a E(X(Y-X))=E(X)E(Y-X)

pourtant on peut rien conclure si la variance est différente de 0 ...

[alavacommejetepousse]

bonjour tu peux stp me la calculer ? merci d'avance !!

bonjour

as tu réussi cette partie ?

[MathMoiCa]

Salut,

Tu peux utiliser cette propriété (formule de transfert) :

Le couple (X,Y) a la densité g si et seulement si pour toute fonction borélienne bornée h,

Applique ça à en disant que c'est une certaine fonction appliquée au couple (X,Y), puis fais un changement de variable (Jacobien) u=x, v=x-y, et vois si la densité s'écrit comme le produit de deux densités.


M.

[sniperamine]

Salut,

Tu peux utiliser cette propriété (formule de transfert) :

Le couple (X,Y) a la densité g si et seulement si pour toute fonction borélienne bornée h,

Applique ça à en disant que c'est une certaine fonction appliquée au couple (X,Y), puis fais un changement de variable (Jacobien) u=x, v=x-y, et vois si la densité s'écrit comme le produit de deux densités.


M.

Bonsoir mathsmoica merci pour ton aide mais c'est la méthode un peu "bourrine" dont nous avons parlé lol

[MathMoiCa]

Ouais mais bon t'es mignon de penser que ça peut se faire sans calculs...
Et là, le calcul n'a vraiment rien de difficile, étant donné que c'est une transfo linéaire, donc jacobien égal à une constante, donc pas énormément de calculs...
Flemmard va ! :D


M.