Lois de composition
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 21 Mai 2012, 15:56
par Dinozzo13 » 21 Mai 2012, 15:56
Salut !
Un isomorphisme est un morphisme bijectif.
On dit qu'une application

du groupe
)
dans le groupe
)
est un morphisme de groupe si et seulement si pour tout
=f(x) \nabla f(y))
.
Un endomorphisme est un morphisme de E dans lui même.
Un automorphisme est un isomorphisme et un endomorphisme.
-
lexioou
- Membre Naturel
- Messages: 32
- Enregistré le: 07 Nov 2010, 19:03
-
 par lexioou » 21 Mai 2012, 16:05
par lexioou » 21 Mai 2012, 16:05
Je prends note mais avec l'exercice que j'ai cité plus haut, je ne sais pas comment arriver à prouver que c'est un morphisme je fais ceci:
f(x)x(y)=(1-(1/x))(1-(1/y)) et je fais les calculs
mais après avec f(x*y) je sais pas comment faire!

-
alm
- Membre Relatif
- Messages: 335
- Enregistré le: 15 Jan 2009, 01:00
- Localisation: Salé, Maroc
-
 par alm » 21 Mai 2012, 16:56
par alm » 21 Mai 2012, 16:56
Salut;
Puisque tu n'as pas donné la definition de

, la question logique est de dire:
Définir la lois

sachant qu'il s'agit b d'un isomorphisme
on pose
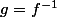
Justement
 g(y) = g(x*y))
nous donne
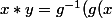g(y)))
or
= 1-(1/x))
donne
=f^{-1} (x)= \frac{1}{1-x})
Je te laisse trouver

-
lexioou
- Membre Naturel
- Messages: 32
- Enregistré le: 07 Nov 2010, 19:03
-
 par lexioou » 21 Mai 2012, 17:31
par lexioou » 21 Mai 2012, 17:31
Re-bonjour!
Merci beaucoup de ton aide et de tes explications et je vais essayer de faire beaucoup d'exercices, histoire que ça rentre une bonne fois pour toutes ^^
Finalement merci à tous :)

-
alm
- Membre Relatif
- Messages: 335
- Enregistré le: 15 Jan 2009, 01:00
- Localisation: Salé, Maroc
-
 par alm » 21 Mai 2012, 17:41
par alm » 21 Mai 2012, 17:41
Je t'en prie mais tu peux toujurs revenir au cas du besoin!
N'hésite pas alors !
-
lexioou
- Membre Naturel
- Messages: 32
- Enregistré le: 07 Nov 2010, 19:03
-
 par lexioou » 21 Mai 2012, 19:47
par lexioou » 21 Mai 2012, 19:47
Bonsoir,
Je suis de retour ^^ J'ai encore du mal avec certains exercices --'
Pour l'exercice qui suit on nous demande de montrer que f est un automorphisme et j'y arrive pas du tout :/
pour tout (x,y) E R² f(x,y)=(x,e^(x)-e^(-x)+y)
Merci beaucoup de votre aide :)
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 21 Mai 2012, 19:52
par Dinozzo13 » 21 Mai 2012, 19:52
Salut !
Quelles sont les opérations mises en jeu ?
-
lexioou
- Membre Naturel
- Messages: 32
- Enregistré le: 07 Nov 2010, 19:03
-
 par lexioou » 21 Mai 2012, 20:06
par lexioou » 21 Mai 2012, 20:06
Dinozzo13 a écrit:Salut !
Quelles sont les opérations mises en jeu ?
Soit l'application f de (R²,*) dans lui même.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 21 Mai 2012, 20:15
par Dinozzo13 » 21 Mai 2012, 20:15
Montre que
=f(x)*f(y))
pis que

est bijective :++:
-
lexioou
- Membre Naturel
- Messages: 32
- Enregistré le: 07 Nov 2010, 19:03
-
 par lexioou » 21 Mai 2012, 20:36
par lexioou » 21 Mai 2012, 20:36
Re-bonsoir
Je trouve alors:
f(x*y)=f[(x,y)*(x',y')]=(x,e^(x)-e^(-x)+y)*(x',e^(x')-e^(-x')+y')=x+x',e^(x)-e^(-x)+y*e^(x')-e^(-x')+y'=(x,e^(x)-e^(-x)+y)*(x',e^(x')-e^(-x')+y)=f(x,y)*f(x',y')
Est ce que c'est juste? :)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités