Lois de composition

[lexioou]

Enoncé: Soit E=[0,1] on définit une loi * sur E par pour tout x,y appartenant à E, x*y=x+y-xy
a)Montrer que * est une loi de composition interne commutative et associative.

Résolution du a) 1-(x+y-xy)=(1-x)(1-y) donc si x<=1 et y<=1 alors x*y<=1 par suite * est bien une loi de composition interne sur * et est clairement commutative et associative.

Je ne comprends pas cette explication si quelqu'un peut m'apporter de l'aide, parce que normalement pour voir si elle est, par exemple, commutative on fait x*y et y*x et on regarde si c'est pareil non?

Merci de votre aide et de votre temps

[Euler07]

Coucou

Le truc c'est qu'il ont pas montrer la commutativité de façon algébrique (du fait de l'évidence) puisque les x et y jouent des rôles symétriques, idem pour l'associativité
Dans tout les cas comme l'ensemble en question est E = [0,1], il faut néanmoins montrer que la loi * est bien définie c'est à dire reste bien dans E

:livre:

[lexioou]

Ce que je ne comprends pas c'est pourquoi il y a un 1 => 1-(x+y-xy) alors que x*y=x+y-xy ?

[lexioou]

Et puis au début on nous demande de montrer que x+y-xy est différent de 1 avec comme indication que 1-xy+xy=(1x)(1-y)!
Cela peut venir de là?

[Euler07]

On veut montrer que x+y-xy est dans E, donc plus petit que 1 (puisque E = [0,1])
1 - (x+y-xy) donne bien (1-x)(1-y) est comme ce terme obtenu est positif donc 1 > x+y-xy

:livre:

[lexioou]

On veut montrer que x+y-xy est dans E, donc plus petit que 1 (puisque E = [0,1])
1 - (x+y-xy) donne bien (1-x)(1-y) est comme ce terme obtenu est positif donc 1 > x+y-xy

:livre:

Ah oui d'accord, je comprends mieux, merci beaucoup de ton aide :lol3:

[Dinozzo13]

Salut !

Salut Euler07 :++:

Il s'agit là d'un exo classique ! Je suis déjà tombé dessus ^^

[Euler07]

Salut !

Salut Euler07 :++:

Il s'agit là d'un exo classique ! Je suis déjà tombé dessus ^^

Oui ton partiel tu m'avais même demandé à faire

:livre:

[lexioou]

Par contre j'ai du mal à déterminer l'élément neutre :/
Si vous pouviez m'aider :)

[Euler07]

L'élément neutre doit vérifier x*e = x (l'autre sens aussi, mais puisque * est commutative)
Généralement 0 ou 1 voir -1 marche bien, essaye de voir ;)

:livre:

[alm]

Bonsoir:

L'élément neutre doit vérifier x*e = x (l'autre sens aussi, mais puisque * est commutative)
Généralement 0 ou 1 voir -1 marche bien, essaye de voir

:livre:

C'est l'élément neutre.
Une méthode pour le chercher (avant de l'avoir connu)
Supposons que e est le neutre
alors or d'où 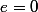Réciproquement pour tout on a et la lois est commutative
Conclusion : est le neutre

Deux remarques :
Remarque 1:
Généralement, si l'élément neutre d'un ensemble muni d'une loi interne existe alors il est unique.
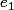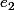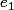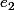Preuve: si et sont deux neutres alors car est neutre et car est neutre , par suite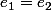

Remarque2:
Concerne cet exercice : l'application tele que est un isomorphisme de vers (il est déjà dit dans la relation en haut : ensuite est manifestement bijective )
Cet isomorphisme permet de savoir que est associative (commutative c'est facil à voir) et que l'élément neutre est (remarque 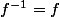, donc involutive).
Cet isomorphisme peremt aussi de savoir que est le seule élément symétrisable dans . En effet , est le seul élément inversible dans

[Euler07]

Pour la remarque 2, tu veux parler de transfère de la structure de groupe ?

:livre:

[alm]

Pour la remarque 2, tu veux parler de transfère de la structure de groupe ?

:livre:

Oui Euler : transfert oui
mais transfert de structure pas forcément de groupe
en effet il ne s'agit pas encore d'un groupe car est le seul inversible ...

[Euler07]

En gros tu as utilisé l'injectivité de f pour trouver que 0 est neutre :we: ?

:livre:

[alm]

En gros tu as utilisé l'injectivité de f pour trouver que 0 est neutre :we: ?

:livre:

oui on a besoin de l'isomorphisme réciproque (en l'occurence f lui même pour partir de l'arrivée) mais il était possible d'y remédier en considérant avec ( ce n'est qu'une coincidence d'avoir la même expression pour f et g)

La régle générales étant : si est un morphisme et si e est le neutre pour alors est le neutre pour .
Si en plus f est surjective alors est le neutre pour

Quand est bijective (comme notre cas) il y vas et viens (les deux sens).

[Euler07]

Je pensais plutôt au fait que Ker f = e' l'ensemble des x de E tels que f(x) = e', ici e' serait 1

:livre:

[alm]

Je pensais plutôt au fait que Ker f = e' l'ensemble des x de E tels que f(x) = e', ici e' serait 1

:livre:

ah ok , mais c'est un autre sujet
Par exemple l'application (déterminant) est un morphisme de matrice inversible (réelles) de taille vers et comme la matrice unité est le neutre de son image est le neutre de
Cependant n'est pas réduit à mais (le groupe spécial dont les éléments sont les matrices de determinant , par exemple une matrice triangulaire dont la diagonale comprends des 1 sauf pour deux termes qui valent et où quelconque ... ou tout simplement les matrices de transvections sont des éléments de )

[lexioou]

Excusez moi mais est ce quelqu'un peut m'expliquer ce qu'est clairement un morphisme endomorphisme isomorphisme et automorphisme j'ai vraiment du mal avec le cours et encore plus sur des exercices et si possibles quelques exemples parce que je saisis pas du tout :/
Merci de votre aide et de votre temps :)

[alm]

Salut,

Est ce une autre questionq?
Je pose la question pour ma rassurer que tu as déjà compris les reponses donnée au sujet de ta question au debut de ce topic

[lexioou]

Re-bonjour !
Oui j'ai finalement bien compris :) mais c'est que j'ai un petit problème au niveau des morphismes et le reste comme j'ai pu vous le dire au message précédent, je n'arrive pas à trouver le morphisme de l'exercice suivant:
f: R\(0) => R\(1) l'application définie par f(x)=1-(1/x).
On munit l'ensemble R\(0) de la multiplication et l'autre ensemble de l'opération *. Montrer que f est un isomorphisme. Donc d'après mon cours l'isomorphisme est un morphisme bijectif? ( ou il faut juste que f soit bijectif?)
Si je montre que c'est un morphisme je me retrouve avec du f(x)f(y)=f(x*y) mais ce n'est absolument pas la même chose donc pas un morphisme, enfin j'ai un petit peu de mal :/