Loi pareto
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ditans
- Membre Relatif
- Messages: 107
- Enregistré le: 15 Aoû 2009, 17:27
-
par ditans » 17 Fév 2010, 15:51
Bonjour,
Ceci concerne une question dans un problème sur la loi de pareto.
 = \frac{\alpha}{r_0} (\frac{r_0}{x})^{\alpha + 1} si x \geq r_0)
elle vaut 0 sinon
On me demande de calculer l'espérance E(X) =
 dx)
Donc je remplace et j'obtiens l'intégrale suivante.
Il faudrait que je trouve une primitive de ca.
^{\alpha}dx)
Mais j'ai essayé, et je ne trouve pas ...
Merci de m'aider si possible.
Bonne journée
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
par Nightmare » 17 Fév 2010, 15:59
Salut,
cela dépend un peu de qui est
.
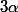
S'il est > 1, une primitive de
est donnée par
x^{\alpha-1}})
S'il est =1, une primitive est
)
S'il est >1, on a une polynôme.
Dans les deux derniers cas, ton intégrale est divergente, donc je suppose qu'on est dans le premier cas !
-
ditans
- Membre Relatif
- Messages: 107
- Enregistré le: 15 Aoû 2009, 17:27
-
par ditans » 17 Fév 2010, 16:15
Merci beaucoup et donc
en prenant
> 1 je trouve que E(X)=
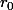
cava ou pas ? :hein:
-
ditans
- Membre Relatif
- Messages: 107
- Enregistré le: 15 Aoû 2009, 17:27
-
par ditans » 18 Fév 2010, 17:43
est-ce qu'il ya quelqu'un qui voudrait bien me dire, si cela est juste ... Car j'ai un gro doute...
je trouve
^{\alpha} \frac{1}{(\alpha -1)x^{\alpha-1}})
comme primitive que je simplifie et que je fais tendre vers +00 et
-
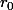
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
par girdav » 18 Fév 2010, 17:57
On a :
^{a+1}\,dx <br />= \int_1^{+\infty}a r_0 t \fr 1{t^{a+1}} \,dt=ar_0\int_1^{+\infty}\fr 1{t^a}\, dt= \fr{a r_0}{a-1})
-
ditans
- Membre Relatif
- Messages: 107
- Enregistré le: 15 Aoû 2009, 17:27
-
par ditans » 18 Fév 2010, 18:17
girdav a écrit:On a :
Merci, tu fais un cchangement de variable là? Et tu en fais quoi du
car je comprends que l'on simplifie ... mais ta puissance est partie ... Enfin je pense que ca soit ca, ca correspond assez avec ce qu'il y a apres dans les exercices mais c'est juste pour comprendre!
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
par girdav » 18 Fév 2010, 18:22
Oui, je ne l'ai pas précisé : j'ai posé
.
-
ditans
- Membre Relatif
- Messages: 107
- Enregistré le: 15 Aoû 2009, 17:27
-
par ditans » 18 Fév 2010, 19:38
bonsoir, alors plus loin dans le problème je rencontre de nouveau une difficulté. En plus c'est frustrant car j'ai l'impression de ne pas voir quelque chose.... Voilà de quoi il s'agit
)
b un parametre reel strictement positif
j'ai déjà montré que la série de terme général
}))
est convergente (n superieur ou égale à 1)
On pose
}))
en admettant que
 = \bigsum_{n=1}^{+\infty} \frac{x^n}{n})
Il s'agit de montrer que
ln(1-e^{-b}))
alors en fait il s'agit de montrer que
}{n(n+1)}) = (1-e^b)ln(1-e^{-bn}))
Et donc là je ne vois surtout pas comment je peut obtenir
Merci de nouveau pour votre aide !
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
par girdav » 18 Fév 2010, 19:50
Décomposes en éléments simples et somme les deux séries que tu obtiendra à l'aide de la formule que tu as sur le logarithme.
-
ditans
- Membre Relatif
- Messages: 107
- Enregistré le: 15 Aoû 2009, 17:27
-
par ditans » 18 Fév 2010, 20:07
oui merci, c'est ce que j'ai essayé. C'est facile quand c'est juste
n})
mais là avec l'exponentielle je n'y arrive pas. D'autant plus que ce n'est pas dans mon programme car je ne suis pas en prépas scientifique. (économique)
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
par girdav » 18 Fév 2010, 20:11
Que te donne la décomposition en éléments simples?
-
ditans
- Membre Relatif
- Messages: 107
- Enregistré le: 15 Aoû 2009, 17:27
-
par ditans » 18 Fév 2010, 20:56
girdav a écrit:Que te donne la décomposition en éléments simples?
} = \frac{1}{n}+\frac{1}{n+1})
mais je ne sais pas quoi faire de
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
par girdav » 18 Fév 2010, 21:03
Pose
. D'ailleurs, ça me fait penser que dans la dernière formule du message #8 je crois qu'il ne devrait pas y avoir de
dans le membre de droite de la toute dernière formule.
-
ditans
- Membre Relatif
- Messages: 107
- Enregistré le: 15 Aoû 2009, 17:27
-
par ditans » 19 Fév 2010, 10:45
Bonjour
oui tu as raison, il y a un n en trop. Merci en tout cas pour ta réponse.
Sinon j'ai trouvé
}= \frac{1-x^n}{n} + \frac{x^n-1}{n+1})
mais il me semble que cela soit plutôt inutile! =S
-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
par Ben314 » 19 Fév 2010, 11:27
Effectivement, ce n'est pas super utile...
Commence par "couper" ta série en deux séries (convergentes) :
}\ =\ \bigsum_{n=1}^{+\infty} \frac{1}{n(n+1)}\ -\ \bigsum_{n=1}^{+\infty} \frac{e^{-bn}}{n(n+1)})\ =\ S_1-S_2)
puis utilise le fait que
}=\frac{1}{n}-\frac{1}{n+1})
.
Attention pour la première série à ne pas écrire :
}\ =\ \bigsum_{n=1}^{+\infty} \frac{1}{n}\ -\ \bigsum_{n=1}^{+\infty} \frac{1}{n+1})
car les deux sommes sont divergentes !!!
On écrit donc :
}\ =\ \bigsum_{n=1}^{A} \frac{1}{n}\ -\ \bigsum_{n=1}^{A} \frac{1}{n+1}=\left(\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{A}\right)-<br />\left(\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+ \frac{1}{A+1} \right)\ =\ 1-\frac{1}{A+1})
et on en déduit en faisant tendre
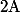
vers
que
Pour
on peut écrire
}\ =\ \bigsum_{n=1}^{+\infty} \frac{e^{-bn}}{n}\ -\ \bigsum_{n=1}^{+\infty} \frac{e^{-bn}}{n+1})
car les deux séries sont convergentes.
La première vaut
^n}{n}\ =\ -\ln(1-e^{-b}))
grâce à l'indication.
La deuxième vaut
^n}{n+1}\ =\ \bigsum_{m=2}^{+\infty} \frac{(e^{-b})^{m-1}}{m}\ =\ \bigsum_{m=1}^{+\infty} \frac{(e^{-b})^{m-1}}{m}-\frac{(e^{-b})^{1-1}}{1})
^m}{m}-1\ =\ -e^b\ln(1-e^{-b})-1)
grâce à l'indication.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
ditans
- Membre Relatif
- Messages: 107
- Enregistré le: 15 Aoû 2009, 17:27
-
par ditans » 19 Fév 2010, 12:39
merci! et la limite en 0 de ce qu'on trouve, ca vaut bien 0 non ? car c'est indéterminée il me semble...
merci! Bonne journée
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
par girdav » 19 Fév 2010, 17:28
ditans a écrit:Bonjour
oui tu as raison, il y a un n en trop. Merci en tout cas pour ta réponse.
Sinon j'ai trouvé
mais il me semble que cela soit plutôt inutile! =S
Je voulais faire cela avec le second terme de la somme c'est-à-dire
}=\fr 1{n\(n+1\)}-x^n\fr{1}{n\(n+1\)})
.
C'est sans doute la fait de ne pas avoir précisé ça qui a rendu mon indication assez peu claire.
Mais je vois que Ben314 m'a précédé.
-
ditans
- Membre Relatif
- Messages: 107
- Enregistré le: 15 Aoû 2009, 17:27
-
par ditans » 19 Fév 2010, 19:30
oui merci, je croyais que tu voulais un truc plus compliqué... Mais vraiment merci en tout cas!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités
