Bonjour,
Je voudrais savoir s'il est possible de tracer une loi normale quand on n'a que quelques données de connues ?
Je m'explique. Sur une population de produits bien définie, quelques-uns commencent à tomber en panne. On sait très bien qu'ils vont tous devenir HS tôt ou tard dans les mêmes circonstances. Cette fin de vie prématurée entre bien dans le cas de la loi normale. En faisant le compte du nombre de produits qui tombent en panne par mois, on se retrouve avec un début de courbe exponentielle.
Est-il possible de continuer cette courbe par des calculs, afin de trouver une date approximative où la moitié de la population sera HS ou encore pour savoir vers quelle date la population entière le sera ?
Désolé pour tout le blabla, j'espère que je me suis bien exprimé. :marteau:
Merci d'avance.
Loi normale
5 messages
- Page 1 sur 1
Salut,
oui, ca s'appelle de la statistique, tu vas estimer les parametres de la loi normale.
Tu pourrais appliquer la methode du maximum de vraissemblance mais le plus rapide ici et le plus simple est encore d'appliquer la methode des moments(l'estimateur de la moyenne est le meme en plus je crois).
donc:
tu fais la moyenne empirique de tes valeurs, ce sera la valeur de ton parametre m.
Tu calcules la variance empirique de ton echantillon ce sera ta variance V.
Tu n'as plus qu'a tracer la densité de la loi normale N(m,V).
oui, ca s'appelle de la statistique, tu vas estimer les parametres de la loi normale.
Tu pourrais appliquer la methode du maximum de vraissemblance mais le plus rapide ici et le plus simple est encore d'appliquer la methode des moments(l'estimateur de la moyenne est le meme en plus je crois).
donc:
tu fais la moyenne empirique de tes valeurs, ce sera la valeur de ton parametre m.
Tu calcules la variance empirique de ton echantillon ce sera ta variance V.
Tu n'as plus qu'a tracer la densité de la loi normale N(m,V).
Hmm oui je vois attends. Tu as raison dans ton cas ce ne sont pas des données collectées aléatoirement que tu mesures mais tu cherches a reconstituer la repartition normale avec les bons parametres en ayant qu'une partie des données(obtenu de facon non aleatoire, en l'occurence tu ne vois qu'une partie de la courbe). Estimer statistiquement les parametres donnerait ici des resultats aberrants.
On pourrait faire une regression:
tu chercherais la courbe representant la densité d'une loi normale qui minimise la somme des ecarts aux carrés, la courbe normale des moindres carrés.
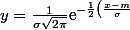^2})
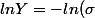 +ln ( \sqrt{2\pi}) -\frac{1}{2}\left(\frac{x-m}{\sigma}\right)^2)
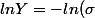 +ln ( \sqrt{2\pi}) -\frac{1}{2}\left(\frac{x^2+m^2-2mx}{\sigma^2}\right))
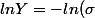 +ln ( \sqrt{2\pi}) -\frac{1}{2}\left(\frac{m^2}{\sigma^2}\right)+\frac{1}{2}\left(\frac{2m}{\sigma^2}\right)x-\frac{1}{2}\left(\frac{x^2}{\sigma^2}\right))
comme tu le vois meme apres le passage au log difficile d'extraire une linearité des coefficients m et . Et si c'etait calculer ca de facon brute(en minimisant la norme des ecarts et en retournant au moindre carrées) la fonction n'aurait pas forcement un minimum et le calculer necessiterait de toute facon une resolution numerique car a mon avis la sol serait assez chiante a trouver...
. Et si c'etait calculer ca de facon brute(en minimisant la norme des ecarts et en retournant au moindre carrées) la fonction n'aurait pas forcement un minimum et le calculer necessiterait de toute facon une resolution numerique car a mon avis la sol serait assez chiante a trouver...
C'est assez difficile en pratique. Il faudrait chercher une allure plus simple car (bien que je n'ai jamais eu l'occasion de le faire) la gaussienne me semble peu adaptée a la regression, en tout cas ca n'a pas l'air trivial.
Il y avait un petit logiciel dont quelqu'un avait fournit le lien qui faisait des regressions pas mal et pour des fonctions aux modeles assez compliqués. Si quelqu'un a tjs le lien, je pense que ca pourrait t'aider.
Ps: Tu peux toujours faire ca a tatillon hein... T'auras une solution agréable. Tu fais varier les parametres jusqu'a ce que ca epouse au maximum l'allure de tes points. Pour le m tu cherches a mettre la moyenne qui te semble juste et pour le tu ajustes en faisant evoluer la variance.
tu ajustes en faisant evoluer la variance.
On pourrait faire une regression:
tu chercherais la courbe representant la densité d'une loi normale qui minimise la somme des ecarts aux carrés, la courbe normale des moindres carrés.
comme tu le vois meme apres le passage au log difficile d'extraire une linearité des coefficients m et
C'est assez difficile en pratique. Il faudrait chercher une allure plus simple car (bien que je n'ai jamais eu l'occasion de le faire) la gaussienne me semble peu adaptée a la regression, en tout cas ca n'a pas l'air trivial.
Il y avait un petit logiciel dont quelqu'un avait fournit le lien qui faisait des regressions pas mal et pour des fonctions aux modeles assez compliqués. Si quelqu'un a tjs le lien, je pense que ca pourrait t'aider.
Ps: Tu peux toujours faire ca a tatillon hein... T'auras une solution agréable. Tu fais varier les parametres jusqu'a ce que ca epouse au maximum l'allure de tes points. Pour le m tu cherches a mettre la moyenne qui te semble juste et pour le
Salut,
tu peux essayer une estimation avec la droite de Henry.
L'idée est de linéariser la fonction de répartition de la loi normale.
Tu calcules la proportion de valeurs inférieures à tes données. En fait une évaluation de) .
.
A l'aide d'une table de la loi normale tu leur fait correspondre une valeur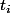 de la loi normale centrée réduite.
de la loi normale centrée réduite.
Si on a à faire avec une loi normale, il y a une relation linéaire entre les et les
et les 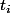 :
:  ,
,
où est l'espérance de la loi normale et
est l'espérance de la loi normale et  son écart-type. Une régression linéaire permet alors l'évaluation de
son écart-type. Une régression linéaire permet alors l'évaluation de  et
et  .
.
Ceci étant je te répond après avoir arrosé la victoire de l'Argentine.
Ce qui rend mes propos douteux.
Et je n'ai jamais rien lu sur la qualité des résultats obtenus.
tu peux essayer une estimation avec la droite de Henry.
L'idée est de linéariser la fonction de répartition de la loi normale.
Tu calcules la proportion de valeurs inférieures à tes données. En fait une évaluation de
A l'aide d'une table de la loi normale tu leur fait correspondre une valeur
Si on a à faire avec une loi normale, il y a une relation linéaire entre les
où
Ceci étant je te répond après avoir arrosé la victoire de l'Argentine.
Ce qui rend mes propos douteux.
Et je n'ai jamais rien lu sur la qualité des résultats obtenus.
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
