Loi du min de 2 va discretes

[olive1978]

Bonjour,

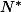
J'ai un va discrete a valeurs dans et un .
On me demande de déterminer la loi de . J'ai fait comme ca, mais j'ai un doute :


Soit, le produit des lois. Est ce bien ca ?
Par ailleurs, a-t-on :


?

[fahr451]

bonjour

non

P(AUB) n 'est pas P(A).P(B)

[olive1978]

bonjour

non

P(AUB) n 'est pas P(A).P(B)

Oui, tu as raison. Et ca :



Donc, pas le produit, mais la somme des deux lois.

[fahr451]

pas plus

P(AUB) = P(A)+P(B) -P(AinterB)

[olive1978]

oula, je dis n'importe quoi aujourd'hui ...
En passanat par les foncions de repartition, j'arrive a qqchose, mais je ne vois pas comment repasser a la loi :



Et d'ailleurs, est ce qu'on peut faire sans passer par les fonctions de repartition ?

[fahr451]

et si tu distinguais 3 situations

k > n0 , K
(sinon pour le cas général du min de deux var indépendantes on passe tjrs par la fct de survie (ou anti répartition) : P( Q> q) )

[olive1978]

(sinon pour le cas général du min de deux var indépendantes on passe tjrs par la fct de survie (ou anti répartition) : P( Q> q) )

C'est ce qui m'a permis d'arriver au resultat precedent. Pour le reste, je vois pas ...

[fahr451]

1 remarque min (n0, X) =< n0

si *) k > n0 {Y = k} = vide
**) k ***) k = n0 { Y=n0} = { X >= n0}

[BQss]

Il y a une reponse simple et clair:

P(Y=k)= P(min(X,n0)=k inter X>=n0) + P(min(X,n0)=k inter Xpartitionnement

P(Y=k)=P(n0=k inter X>=n0) + P(X=k inter X
P(Y=k)= P(X>=n0)*1{n0=k} + P(X=k)*1{k independance avec une variable aleatoire constante (deterministe on dit aussi).

resultat donc:
P(Y=k)= P(X>=n0)*1{n0=k} + P(X=k)*1{k

[fahr451]

c'est kestckegédi on dirait

[BQss]

c'est kestckegédi on dirait

j'en suis sur . Je l'ecrivais explicitement pour mettre fin a son tourment.
Tu ne m'en veux pas j'espere.

[BQss]

La question est deja un peu plus marrante avec X une variable continue admettant une densité. C'est plus instructif et on voit vraiment le saut en n0.

la densité vaut celle de la variable x sur ]-infini;n0[ et en n0, la masse est infini car la variable min(x;n0)=y prend toute la masse de l'ensemble {x>=n0}.

On voit bien que si x est plus grand que n0, le minimum c'est n0, donc la probabilité que min(x;n0)=n0 vaut P(x>=n0).

Avant cette valeure, la probabilité croit continument avec une densité de fx, au point n0 la densité est infini et P(Y=n0)=P(X>=n0).

[BQss]

Un petit graphe avec n0 arbitraire et X suivant une loi normale.