Loi Marginales

[gbsatti]

Bonsoir, j'ai une question qui me barre la route dans un exercice.

Soit (X,Y) un couple de variables aléatoires dont la loi admet la densité:

si 0<x<y<
sinon

1) X et Y sont-elles indépendantes ?

J'ai mis non car x<y

2) Déterminer les loi marginales de X et de Y.

Premièrement j'ai commencé par hiérarchiser le domaine. J'ai obtenu

0<x< et x<y< après avoir fait un dessin du domaine.

Donc j'utilise la formule pour les loi marginales.





Mais il parait que mon est faux. Est-ce que quelqu'un peut m'expliquer où est-ce que j'ai faux car j'ai vérifié plusieurs fois..

Merci

[girdav]

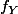
L'intégrale de (il manque d'ailleurs une indicatrice) est , ce ne peut être une densité.

Pour l'indépendance, il faut détailler un peu plus.

[gbsatti]

pour l'indépendance x<y ce qui veut dire que x est liée à y donc les variables ne sont pas indépendantes . Est-ce que c'était le détail manquant ?

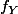
Et sinon je viens de m'apercevoir qu'en effet c'est bête d'écrire sans avoir vérifié que la densité valait 1. Mais je ne vois toujours pas d'où peut provenir le problème...
Pourtant j'ai bien dessiné mon domaine ..
pourrais-tu me donner une piste ?

[girdav]

C'est l'idée, en fait si X et Y étaient indépendantes alors la densité de (X,Y) s'écrirait comme un produit d'une fonction de x avec une fonction de y, donc l'indicatrice de \{(x,y), 0
Concernant le calcul de la seconde loi marginale, je ne sais pas, il faudrait que tu présente le calcul.

[gbsatti]

ah oui je comprend mieux le raisonnement pour ce qui est de l'indépendance maintenant !

Pour le calcul de

[girdav]

Attention, il faut intégrer pour allant de 0 à y.

[gbsatti]

Attention, il faut intégrer à partir de .

ah bon, et pourquoi ? mon domaine pour x j'ai trouvé que c'est ]0,+oo[ ...

et j'ai beaucoup travaillé le cours sur la hiérarchisation du domaine pour les intégrales et x ne doit pas dépendre de y ;.

[girdav]

Pardon, je voulais dire pour x allant de 0 jusqu'à y.

[gbsatti]

comment trouves-tu ça ? moi j'ai dessiné le domaine et j'ai x dans ]0,oo[ ..

[girdav]

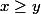
Même sans faire de dessin, fixe . La densité du couple est nulle si , donc ça ne sert à rien d'intégrer au delà.

[gbsatti]

désolé mais j'ai un peu la tête dure :marteau:
peux-tu m'expliquer mieux s'il te plait? J'ai l'habitude à ce que le domaine de la première variable (ici x) ne dépende pas la seconde (y). En revanche y peut être dépendant de x. Bien sur avec le théorème de fubini on peut inverser l'ordre de l'intégration.
Par contre ici ça m'intrigue que x dépende de y et l'inverse...

[girdav]

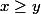
est fixé, on doit intégrer sur par rapport à . Mais on sait que cette quantité est nulle si , donc il suffit d'intégrer entre et . Je ne doute pas que tu saches calculer .

[gbsatti]

merci beaucoup je viens de comprendre, j'avais en effet oublié le détail y fixé ^^.

Bonne soirée :)