Loi de composition pcgd neutre
17 messages
- Page 1 sur 1
Loi de composition pcgd neutre
Bonjour,
Je me présente maclayne, je reprend actuellement mes études et revois les bases en mathématiques.
Je bloque actuellement sur une remarque d'un livre qui dit:
la loi "pgcd" ne possède pas d'élèment neutre.
J'ai cherché à en faire la preuve par l'absurde mais je n'y arrive pas.
Pourriez vous m'aider s'il vous plait.
Je me présente maclayne, je reprend actuellement mes études et revois les bases en mathématiques.
Je bloque actuellement sur une remarque d'un livre qui dit:
la loi "pgcd" ne possède pas d'élèment neutre.
J'ai cherché à en faire la preuve par l'absurde mais je n'y arrive pas.
Pourriez vous m'aider s'il vous plait.
Re: Loi de composition pcgd neutre
Bonjour,
si la loi PGCD avait un élément neutre, noté , on aurait
, on aurait  = a) pour tout nombre entier
pour tout nombre entier  ,
,
donc diviserait
diviserait  pour tout entier
pour tout entier  , donc
, donc  serait infiniment grand, en choisissant
serait infiniment grand, en choisissant  arbitrairement grand.
arbitrairement grand.
Amicalement,
si la loi PGCD avait un élément neutre, noté
donc
Amicalement,
Modifié en dernier par Mateo_13 le 26 Fév 2023, 15:32, modifié 1 fois.
Re: Loi de composition pcgd neutre
Bonjour
Si c'est élément e existait il vérifierait pgcd(n,e)=n pour tout entier n
donc n serait diviseur de e quel que soit n donc n<=e pour tout entier n.
e serait le plus grand élément de N or celui ci n'existe pas.
Si c'est élément e existait il vérifierait pgcd(n,e)=n pour tout entier n
donc n serait diviseur de e quel que soit n donc n<=e pour tout entier n.
e serait le plus grand élément de N or celui ci n'existe pas.
Re: Loi de composition pcgd neutre
Bonjour,
Deux réponses rapides, mais deux mauvaises réponses : le pgcd vu comme loi de composition interne sur a bel et bien un élément neutre : 0. Et aussi un élément absorbant : 1.
a bel et bien un élément neutre : 0. Et aussi un élément absorbant : 1.
Rappel de définition est pgcd de
est pgcd de  et
et  si et seulement si
si et seulement si  est un diviseur commun de
est un diviseur commun de  et
et  et que tout diviseur commun de
et que tout diviseur commun de  et
et  divise
divise  .
.
Autrement dit, est pgcd de
est pgcd de  et
et  si et seulement l'ensemble des diviseurs de
si et seulement l'ensemble des diviseurs de  est égal à l'ensemble des diviseurs communs de
est égal à l'ensemble des diviseurs communs de  et
et  .
.
Quel est ce livre qui raconte des bêtises ?
Mateo13 et catamat font d'ailleurs la même erreur de raisonnement :
"donc diviserait
diviserait  pour tout entier , donc
pour tout entier , donc  serait infiniment grand."
serait infiniment grand."
"donc n serait diviseur de e quel que soit n donc n<=e pour tout entier n."
Tout entier divise 0 !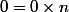
Deux réponses rapides, mais deux mauvaises réponses : le pgcd vu comme loi de composition interne sur
Rappel de définition
Autrement dit,
Quel est ce livre qui raconte des bêtises ?
Mateo13 et catamat font d'ailleurs la même erreur de raisonnement :
"donc
"donc n serait diviseur de e quel que soit n donc n<=e pour tout entier n."
Tout entier divise 0 !
Modifié en dernier par GaBuZoMeu le 26 Fév 2023, 18:23, modifié 1 fois.
Re: Loi de composition pcgd neutre
 mea culpa...
mea culpa...En effet tout entier divise 0 !
Merci GaBuZoMeu d'avoir rectifié.
Re: Loi de composition pcgd neutre
pgcd(e+1,e)=e+1 entraine que e+1 divise e , et donc ((e+1 e)ou(e=0))est vrai
e)ou(e=0))est vrai
or non(e+1 e) est vrai
e) est vrai
donc ((e+1 e)ou(e=0))et (non(e+1
e)ou(e=0))et (non(e+1 e) est vrai
e) est vrai
mais (((p ou q)et(non p)) implique q) est vraie qqs p et q .
donc e=0
or non(e+1
donc ((e+1
mais (((p ou q)et(non p)) implique q) est vraie qqs p et q .
donc e=0
Re: Loi de composition pcgd neutre
On peut peut-être trouver un compromis qui ne fâchera personne. Peut-être que ce bouquin parlait de la loi PGCD définie sur ^2) ?
?
Re: Loi de composition pcgd neutre
Sûr que quand on enlève l'élément neutre d'une loi de composition interne, il y a assez peu de chances pour qu'il en reste un. Un cas où ça se produit tout de même :  avec
avec 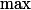 .
.
Re: Loi de composition pcgd neutre
Merci GaBuZoMeu de ne pas m'avoir flingué. Ma lourde réponse n'était qu'un canular.
Je la rédige donc correctement.
Sur c'est élémentaire:
c'est élémentaire:
prérequis: définition et unicité de l'élément neutre.
pgcd(a,b)=pgcd(-a,b)=pgcd(a,-b)=pgcd(-a,-b)
pour tout a dans on a : pgcd(a,e)=a et pgcd(a,-e)=a
on a : pgcd(a,e)=a et pgcd(a,-e)=a
D'après l'unicité du neutre e=-e et donc e=o
réciproquement pour tout a dans on a : pgcd(a,0)=a
on a : pgcd(a,0)=a
cqfd
Sur
Prérequis:
on a sur : si a divise b , alors
: si a divise b , alors 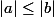 ou b=0
ou b=0
qui devient sur : si a divise b , alors
: si a divise b , alors 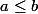 ou b=0
ou b=0
On a donc pgcd(e+1,e)=e+1
Donc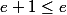 ou e=0
ou e=0
comme e+1 n'est pas inférieur ou égal à e , on a e=0
réciproquement pour tout a dans on a : pgcd(a,0)=a
on a : pgcd(a,0)=a
cqfd
Je la rédige donc correctement.
Sur
prérequis: définition et unicité de l'élément neutre.
pgcd(a,b)=pgcd(-a,b)=pgcd(a,-b)=pgcd(-a,-b)
pour tout a dans
D'après l'unicité du neutre e=-e et donc e=o
réciproquement pour tout a dans
cqfd
Sur
Prérequis:
on a sur
qui devient sur
On a donc pgcd(e+1,e)=e+1
Donc
comme e+1 n'est pas inférieur ou égal à e , on a e=0
réciproquement pour tout a dans
cqfd
Re: Loi de composition pcgd neutre
Déçu que je ne t'aie pas "flingué" ?
Alors allons-y : Comment définis-tu LE pgcd sur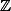 ? Tu prends celui qui est positif ou nul ? Alors tu peux toujours courir pour avoir un élément neutre.
? Tu prends celui qui est positif ou nul ? Alors tu peux toujours courir pour avoir un élément neutre.
Par ailleurs le point délicat est pgcd(0,0). Pour ça il vaut mieux adopter la définition robuste de pgcd.
Alors allons-y : Comment définis-tu LE pgcd sur
Par ailleurs le point délicat est pgcd(0,0). Pour ça il vaut mieux adopter la définition robuste de pgcd.
Re: Loi de composition pcgd neutre
Merci à toi. J'ai en effet dit beaucoup de conneries sans que ce soit un canular.
Par exemple pgcd(a,0)=a sur Z alors que c'est |a| lorsque a est non nul, et pas de définition naturelle pour (0;0) sauf à prendre 0 pour prolonger "pgcd(a,0)=a"
Je manque de temps. je vais relire plus tard ton message 19h02 et je te recontacte.
Par exemple pgcd(a,0)=a sur Z alors que c'est |a| lorsque a est non nul, et pas de définition naturelle pour (0;0) sauf à prendre 0 pour prolonger "pgcd(a,0)=a"
Je manque de temps. je vais relire plus tard ton message 19h02 et je te recontacte.
Re: Loi de composition pcgd neutre
@ GaBuZoMeu 17h06
a b c d e
a a b c d e
b b b c d e
c c c c d e
d d d d d e
e e e e e e
Ceci est la table d'une LDCI définie sur {a,b,c,d,e}X{a,b,c,d,e}
Si on enlève a , b est neutre sur {b,c,d,e}X{b,c,d,e}
Si on enlève a et b , c est neutre sur {c,d,e}X{c,d,e}
etc.
a b c d e
a a b c d e
b b b c d e
c c c c d e
d d d d d e
e e e e e e
Ceci est la table d'une LDCI définie sur {a,b,c,d,e}X{a,b,c,d,e}
Si on enlève a , b est neutre sur {b,c,d,e}X{b,c,d,e}
Si on enlève a et b , c est neutre sur {c,d,e}X{c,d,e}
etc.
Re: Loi de composition pcgd neutre
@ GaBuZoMeu 19h05
Je ne connaissais pas cette belle définition qui prolonge naturellement la définition naturelle.
N'y a t il pas aussi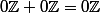 mais ça me parait plus artificiel .
mais ça me parait plus artificiel .
D'autant que l'on a aussi\mathbb{Z})
Il faut donc définir le pgcd de a et b comme le générateur positif de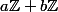
Je ne connaissais pas cette belle définition qui prolonge naturellement la définition naturelle.
N'y a t il pas aussi
D'autant que l'on a aussi
Il faut donc définir le pgcd de a et b comme le générateur positif de
Re: Loi de composition pcgd neutre
L'avantage de la définitiond'un pgcd telle que je l'ai formulée (et qui est très classique) est qu'elle va bien pour tous les anneaux commutatifs intègres (l'existence d'un pgcd n'est pas alors garantie).
J'ai donné plus haut l'exemple de avec la loi de composition interne
avec la loi de composition interne 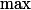 : 0 est élément neutre, si on enlève 0 alors 1 est élément neutre, si on enlève 0 et 1 alors 2 est élément neutre etc.
: 0 est élément neutre, si on enlève 0 alors 1 est élément neutre, si on enlève 0 et 1 alors 2 est élément neutre etc.
Ton exemple est en fait une version tronquée de cet exemple.
J'ai donné plus haut l'exemple de
Ton exemple est en fait une version tronquée de cet exemple.
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
