Loi binomiale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
babaz
- Membre Naturel
- Messages: 71
- Enregistré le: 30 Aoû 2006, 15:07
-
 par babaz » 28 Fév 2010, 19:55
par babaz » 28 Fév 2010, 19:55
Bonsoir,
Soient deux compartiments notés 1 et 2, où se répartissent a molécules, numérotées 1,2,...,a
À chaque instant, une molécule est tirée au hasard et changée de compartiment.
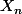 est le nombre de molécules dans le premier compartiment à l'instant n.
est le nombre de molécules dans le premier compartiment à l'instant n.Soit
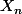
, une chaîne de Markov, dont la matrice de transition P est donc :

En supposant
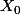
de loi binomiale B(a,1/2), on nous demande de déterminer la loi de
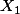
.
Il s'avère alors que la loi de
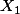
est la même loi binomiale B(a,1/2), mais qu'en déduit-on ?
Je vous remercie
 par alavacommejetepousse » 28 Fév 2010, 22:29
par alavacommejetepousse » 28 Fév 2010, 22:29
bonsoir
on en déduit que la répartition ne dépend pas de la date à laquelle on se place ( c était facile non avec la fpt?)
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 28 Fév 2010, 23:11
par MacManus » 28 Fév 2010, 23:11
Bonjour
Il s'agit du modèle d'Ehrenfest pour a molécules.
On peut montrer d'une manière générale que pour a molécules, il existe une unique loi stationnaire

binomiale de paramètres a et 1/2 (

~B(a,1/2), où ~ signifie : suit la loi ).
Si
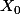
~

, alors pour tout n
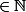
,

~

.
La loi stationnaire correspond à
l'état d'équilibre pour le système.
-
babaz
- Membre Naturel
- Messages: 71
- Enregistré le: 30 Aoû 2006, 15:07
-
 par babaz » 01 Mar 2010, 06:17
par babaz » 01 Mar 2010, 06:17
Merci!
Si l'état d'équilibre est atteint, peut-on dire que cette chaîne "converge" dès le départ ?
Sinon, avez-vous l'impression que cette chaîne est périodique ? Je n'en ai pas l'impression, or, l'une des questions laisse entendre qu'elle l'est...
Merci beaucoup
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 01 Mar 2010, 06:38
par MacManus » 01 Mar 2010, 06:38
Alors je me souviens d'avoir vu cet exemple pour les chaînes de markov, mais je ne l'ai pas sous la main et je n'ai pas les calculs... mais normalement il n'est pas certain qu'il y ait convergence de la suite
)
, où P est ta matrice de transition et
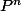
la puissance nième de P, puisque le nombre de molécules est soit pair ou impair, selon le compartiment (de même, on n'a pas nécessairement convergence de la loi de

vers

) : il faut donc considérer la parité de n. C'est à dire qu'on doit regarder les sous-suites
)
et
)
et déterminer leurs limites (qd n tend vers l'infini).
PS : pour calculer la puissance n ième de P, on peut diagonaliser P
-
babaz
- Membre Naturel
- Messages: 71
- Enregistré le: 30 Aoû 2006, 15:07
-
 par babaz » 01 Mar 2010, 06:55
par babaz » 01 Mar 2010, 06:55
La limite de P doit être déduite - c'est ce que suggère la question - de la distribution invariante et de la période de la chaîne...
As-tu l'impression d'avoir ici une chaîne périodique ?
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 01 Mar 2010, 07:07
par MacManus » 01 Mar 2010, 07:07
cette chaîne est périodique de période 2 d'après ce que j'ai pu voir sur le net. En fait, on pourrait le calculer mais j'ai un peu la flemme maintenant. Mais je veux bien le faire un peu plus tard aujourd'hui et confirmer !
-
babaz
- Membre Naturel
- Messages: 71
- Enregistré le: 30 Aoû 2006, 15:07
-
 par babaz » 01 Mar 2010, 07:12
par babaz » 01 Mar 2010, 07:12
Merci beaucoup pour ton aide actuelle et à venir!
J'avais, pour ma part, l'impression initiale que cette chaîne était apériodique, puisque que l'on pouvait passer d'une situation à l'autre, sans qu'il n'y ait le moindre "balancier".
Merci!
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 01 Mar 2010, 07:16
par MacManus » 01 Mar 2010, 07:16
Oui j'ai vu 2-périodique, mais bon il faut se méfier on ne sait jamais.
Je te redis ça dès que je peux ; )
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 01 Mar 2010, 07:58
par MacManus » 01 Mar 2010, 07:58
Bon cette chaîne est irréductibe puisque l'on peut tjrs passer d'un état à un autre (enfin d'un nombre de molécule à un autre).
Oui tu as raison elle semble apériodique puisque tu ne peux pas boucler sur chaque état (cad il n'y a que des 0 sur la diagonale de P).
Donc effectivement tout laisse à croire que la suite
)
converge en loi vers

-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 01 Mar 2010, 08:02
par MacManus » 01 Mar 2010, 08:02
Je dis DES BETISES
cette chaîne n'est pas apériodique car justement il y a que des 0 sur la diagonale. donc il y a un pb pour la convergence
-
babaz
- Membre Naturel
- Messages: 71
- Enregistré le: 30 Aoû 2006, 15:07
-
 par babaz » 01 Mar 2010, 08:35
par babaz » 01 Mar 2010, 08:35
Merci pour ta réponse.
Je ne vois pas comment elle peut être périodique alors que les possibilités de passage, d'un état à l'autre, sont a priori infinies.
Le compartiment 1 peut contenir 2, puis 3, puis 2, puis 3, puis 4, puis 5, puis 4 molécules... tout comme il pourrait en contenir 1, puis 2, puis 1, puis 2, puis 3, puis 4... ?
-
babaz
- Membre Naturel
- Messages: 71
- Enregistré le: 30 Aoû 2006, 15:07
-
 par babaz » 01 Mar 2010, 22:06
par babaz » 01 Mar 2010, 22:06
Salut!
Voici la réponse que j'ai obtenue sur futura-sciences, quant à la période de cette chaîne :
Il me semble plutôt qu'elle est de période 2.
Pour revenir en 1 partant de 1 :
1 puis 2 puis 1 (2 mouvements)
1 puis 2 puis 3 puis 2 puis 1 (4 mouvements)
1 puis 2 puis 3 puis 4 puis 3 puis 2 puis 1 (6 mouvements)
and so on... Le PGCD est 2.
Partant d'un point

qui n'est pas une extrêmité.

puis
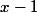
puis

ou

puis
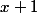
puis

(2 mouvements)

puis
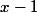
puis
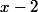
(si possible) puis
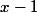
puis

(idem avec des +) (4 mouvements)
et ainsi de suite. Le PGCD est 2.
Qu'en penses-tu ?
Merci!
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 01 Mar 2010, 22:46
par MacManus » 01 Mar 2010, 22:46
Voilà c'est comme ça qu'il faut le voir, je suis d'accord. Cette chaîne est bien irréductible et de période 2.
Rq:
On définit la période
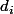
d'un état i comme étant
)
, où
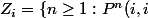>0\})
donc a priori c'est pas si évident.
Ok!
-
babaz
- Membre Naturel
- Messages: 71
- Enregistré le: 30 Aoû 2006, 15:07
-
 par babaz » 01 Mar 2010, 22:50
par babaz » 01 Mar 2010, 22:50
Merci!
Je suis tout à fait désolé mais malgré ton indication, je ne vois pas de quel PGCD il s'agit.
Je ne sais pas si ce que je me disais tient la route, car ça ne semble pas correspondre avec cette définition de la périodicité.
Je pensais qu'une chaîne périodique est une chaîne qui, au bout de k coups, revient obligatoirement à une situation déterminée au tour précédent (à l'image de ce qui se passe avec les fonctions périodiques).

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 01 Mar 2010, 23:04
par Ben314 » 01 Mar 2010, 23:04
Salut,
Comme j'ai pas l'intention de mourrir (trop) idiot et que j'y connait que dalle aux chaines de markof, je suis allé cherché sur internet et... j'ai trouvé les deux définitions possibles...
MAIS, j'ai l'impression que dans les "articles sérieux", c'était celle donnée par MacManus qui dominait.
La période d'un état i peut aussi se lire (de façon équivalente) sur le graphe du processus en regardant le pgcd des longueurs de toutes les boucles partant de i.
Comme chaque étape modifie obligatoirement la parité de X, pour revenir à un état donné, il faut effectivement un nombre pair de transition.
Sinon, je n'ais pas trop compris quel est l'objectif de l'exo...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 01 Mar 2010, 23:19
par MacManus » 01 Mar 2010, 23:19
héhé je crois que j'ai trouvé son sujet, qui se situe vers la fin (en tout cas ça y ressemble beaucoup)
http://pbil.univ-lyon1.fr/R/pdf/AvnerBiol.pdf(Chaîne d'Ehrenfest)
oui voilà tu as très bien résumé la périodicité Ben.
-
babaz
- Membre Naturel
- Messages: 71
- Enregistré le: 30 Aoû 2006, 15:07
-
 par babaz » 02 Mar 2010, 07:26
par babaz » 02 Mar 2010, 07:26
Tu as trouvé mon cours et l'exo associé...
Si les questions qui suivent te tentent, n'hésite surtout pas! -_-
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités


qui n'est pas une extrêmité.
puis
puis
ou
puis
puis
(2 mouvements)
puis
puis
(si possible) puis
puis
(idem avec des +) (4 mouvements)