Logique...
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
baldurs78
- Membre Naturel
- Messages: 28
- Enregistré le: 22 Sep 2006, 12:51
-
 par baldurs78 » 28 Nov 2006, 18:43
par baldurs78 » 28 Nov 2006, 18:43
Bonjour voilà une simple question, pour certains mais j'ai quand même un doute.......
Si

est vrai
et si
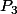
===>
P_5)
est vrai
Est ce qu'on peut dire que
P_5)
est vrai???
Merci bcp !!!!
Bonne soirée
-
humpf
- Membre Relatif
- Messages: 124
- Enregistré le: 01 Nov 2006, 12:53
-
 par humpf » 28 Nov 2006, 19:06
par humpf » 28 Nov 2006, 19:06
Je tente une réponse mais vérifie (je suis vraiment pas la pro en maths :doh: ).
La seconde formule (p3 -> non(p5)) nous donne pour information que si p3 est vrai alors non p5 ne peut pas être faux (il doit donc être vrai).
Maintenant, ta première formule est toujours vraie si p1 est vrai ou p2 est vrai (idem pour celle avec non p5).
Mais, si p1 est faux et p2 est faux alors p3 doit être vrai.
Selon la deuxième formule, si p3 est vrai alors non p5 est forcément vrai donc si ta première formule est toujours vraie alors la troisième est aussi toujours vraie.
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 28 Nov 2006, 23:01
par alben » 28 Nov 2006, 23:01
Bonsoir,
Oui ton affirmation est vraie.
Pour simplifier posons P1 ou P2=Q
La proposition est alors :
[(Q ou P3) et (P3=>nonP5)]=>(Q ou non P5)
soit encore
non[(Q ou P3) et (non P3 ou non P5)] ou Q ou non P5
<=>( nonQ et non P3) ou (P3 et P5) ou Q ou non P5
<=>[( nonQ et non P3) ou Q] ou [(P3 et P5) ou non P5]
en distribuant le "ou" à l'intérieur de chaque [] :
<=>[( nonQ ou Q) et (non P3 ou Q)] ou [(P3 ou non P5) et (P5 ou non P5)]
Les termes (non Q ou Q) ainsi que (P5 ou non P5) peuvent être éliminés et il reste :
<=>[ (non P3 ou Q)] ou [(P3 ou non P5)]
<=> non P3 ou P3 ou Q ou non P5
toujours vrai du fait des deux premiers termes
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités