Dm de logique

[Pierre54]

Bonjour,

je remet l'énoncé, il faut prouver que pour 2-X<2n+1/x+2<2+X, il existe pour tout X>0 un N tel que n>N

[nodgim]

C'est drôle ce par quoi tu as commencé. Comment poursuivre après cette introduction ?
Es tu sûr de ton 2 + X à droite ?
Sinon, tu peux écrire 2n+1 = 2 (n+2) - 3

[zygomatique]

salut

si x > 0 alors u < 2 => u < 2 + x

[Pierre54]

Oui certain de mon énoncé

Justement après quelques indication de ma prof qui me dit d'exprimer N en fonction de X. Je trouve n > 1/X, mais a partir de ça je ne vois pas comment conclure.

A quoi correspond votre "u" ?

Merci

[Ben314]

Salut,
Je pense (ou tout du moins j'espère...) que tu sait résoudre une inéquation du style
ainsi que .
FAIT LE (jusqu'au bout)

Ensuite, ben, tu fait exactement pareil, sauf qu'à la place de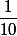 , ben tu écrit X : le réel X est supposé connu donc on calcule avec exactement comme si... il était connu...

[Pierre54]

Oui je sais quand même faire ça, je vais le faire.

Mais enfaite je dois démontrer que " Pour tout X > 0, il existe un N (entier naturel) tel que pour tout (...)"est vrai, ce qui pose problème est le grand "N", l'expression je comprend.

Merci

[Ben314]

FAIT LE (jusqu'au bout)

Et une fois que tu l'aura fait, tu devrait comprendre (ou éventuellement on t'expliquera)

[Pierre54]

Oui j'obtient n>28 et n>-32, donc le N correspond au 37 et -41, donc oui ça semble vrai, suffir de généraliser en remplaçant 1/10 par X.

[Pierre54]

J'ai donc 3/X -2 < n et -3/X - 2 < n

En remplaçant X par 1/10 je retrouve 28 et -32, cela est juste ?

[Ben314]

Sur le principe, ça me semble tout à fait correct (j'ai pas fait les calculs).
Mais y'a quelques truc qui pourraient être améliorés :
- Déjà, et dés le départ, tu cherche les entiers naturels qui vérifient les inégalités, donc des trucs du style n>-32, ça sert pas à grand chose vu que tout les entiers naturels le vérifient.
Et il est plus que probable que, assez tôt dans les calculs, tu ait un truc qui soit très clairement vérifiés par tout entier positif ce qui fait que la suite des calculs ne sert à rien
- Ensuite, même si ça servait à quelque chose le n>-32, il serait "éliminé" par l'autre condition n>28 : tu veut que les deux inégalités soient toutes les deux vrais. Donc tu veut que n>-32 et aussi que n>28 et, clairement ç veut juste dire qu'il faut que n>28 (vu que tout les nombres >28 sont évidement >-32).

Bref, la seule condition que tu as (dans le cas X=1/10), c'est n>28. Donc le N que tu cherche, c'est ce 28 là (dans le cas où X=1/10 bien sûr)

Idem avec le cas général de X quelconque : si n>3/X-2 alors il sera forcément >-3/X-2 donc il suffit de garder l'unique condition n>3/X-2.

[Pierre54]

Ah oui d'accord je comprend ce que vous voulez dire, oui en effet une seul condition suffit et dans mes calculs je vérifie la condition dès le début.

Merci beaucoup pour votre aide !!

[zygomatique]

pourquoi supprimer l'énoncé ? ...

[Pierre54]

pourquoi supprimer l'énoncé ? ...

Pas fait exprès je le remet