Localisation des zéro d'un polynôme

[valentin68000]

bonjour, je suis en prépa MPSI et j'ai un dm à rendre pour lundi, Il me reste un dernier exercice, mais je n'arrive pas à trouver la solution si quelqu'un pourrait m'aider :

soit n ∈ N* on a le polynôme P défini par : P(X)=X^n+an-1X^n-1+...a1X+a0
et on a r une racine de P éventuellement complexe tel que p(r)=0 avec M=max (|ak|) 0≤k<≤n-1
montrer alors que : |r|≤1+M

merci !

[GaBuZoMeu]

Soit tel que . Alors

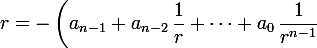Si , on peut en déduire une majoration intéressante de .
Edit : malheureusement ce n'est pas la bonne. Mal lu l'énoncé. Celle-ci, c'est avec le max de 1 et de la somme des modules des .

[GaBuZoMeu]

Bon, je recommence, toujours à partir de l'égalité écrite plus haut.
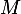
Si , on peut majorer le module du second membre de cette égalité en fonction uniquement de et aboutir à une contradiction.
Je te laisse essayer.

[valentin68000]

j'étais parti à partir du symbole somme pour obtenir M.(1-|r|^n)/1-r mais je ne sais pas non plus comment je pourrais démontrer ceci par l'absurde ...

[GaBuZoMeu]

Relis mon dernier message soigneusement : je parle d'une majoration en terme de uniquement, en supposant .