Bonjour. Pour la question 1, il faut savoir que la somme des probabilités de tous les cas possibles vaut toujours 1.
Ici, il n'y a que deux cas: Soit l'appareil fonctionne (F) Soit il ne fonctionne pas (Non F)
Il faut donc que P(F)+P(NonF)=1 ==> P(NonF)=1-P(F)==> P(NonF)=1-9/10=1/10
Pour la question deux on applique une formule toujours valable du calcul des proba:
=P(A).P(B|A)=P(B).P(A|B))
où P(A) est la proba de l'événement A et P(B|A) celle de B si A s'est produit. Si deux événements sont indépendants, c-à-d que la réalisation de l'un n'influence pas la proba de la réalisation de l'autre on a: P(B|A)=P(B)
Donc pour l'exercice:
=P(F).P(T|F))
P(F)=9/10 et il faut comprendre P(T|F) de la façon suivante: Quelle est la probabilité que l'appareil soit accepté étant donné qu'il fonctionne. Lénoncé dit que un appareil qui fonctionne est toujours accepté, cette proba vaut donc 1 et nous avons:
=\frac{9}{10}.1=\frac{9}{10})
d'autre part il faut aussi calculer
=P(nonF).P(T|nonF))
ici, P(nonF)=1/10 et il faut comprendre P(T|nonF) de la façon suivante: quelle est la proba que l'appareil soit accepté étant donné qu'il ne fonctionne pas. Cette proba est donnée dans l'énoncé et vaut 1/11.
On a bien
=P(nonF).P(T|nonF)=\frac{1}{10}.\frac{1}{11}=\frac{1}{110})
On demande aussi P(T) et P(F|T)
Ici un diagramme en arbre peut être bien utile mais on peut s'en passer.
P(T) est la proba que l'appareil soit accepté. Les deux cas possibles sont:
(l'appareil fonctionne ET il est accepté) OU (l'appareil ne fonctionne pas ET il est accepté)
Les proba de chacun de ses événements a déjà été calculée.
P(l'appareil fonctionne ET il est accepté)=
=9/10)
P(l'appareil ne fonctionne pas ET il est accepté)=
=1/110)
Dans les calculs de proba, lorsqu'il y a un OU entre des événements, on somme les probabilités SI LES EVENEMENTS SONT INCOMPATIBLES (c-a-d qu'ils ne peuvent pas se produire ensemble) ce qui est bien le cas ici car un appareil ne peut pas fonctionner et ne pas fonctionner
Nous avons donc P(T)=9/10+1/110=10/11
et enfin pour le calcul de P(F|T) on repart de la formule de départ:
=P(F).P(T|F)=P(T).P(F|T))
donc `
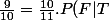)
d'où l'on tire P(F|T)=99/100
Sur tous les appareils ayant réussi le test, nous en auront 99% qui fonctionneront contre 1% qui ne fonctionneront pas.

