Bonjour les mathematiciens
Je dois realiser un modul pour un logiciel qui calcul l'emboitement de credit / lissage
Je n'ai pas trouvé sur internet la reponse a ma question du Comment faire.
Car comme tout les informaticiens si j'ai l algo de calcul je px faire.
Donc je recheche une personne calé en math car je pense que cela est assez difficil a faire( j ai un math sup/spé qui n'a pas reussi a trouver l'algo)
Donc je resume tres rapidement en quoi consiste un lissage de credit
Imaginez que vous voulez acheter la maison de vos reves qui coute 500 000e + 20 000e de travaux
Vous allez voir un courtier immobilier qui vous propose un taux a 4% sur 25 ans soit une mensualité de 2*639,18 ( effectivement dans mon exemple vous etes Directeur :-))
Et pour avoir votre maison de reve l'etat vous file un pret à taux zero de 20 000 e pile poile la somme de vos travaux... ( evidament c fais expres)
Donc le pret a taux zero de l'etat a des caracteristiques!! et oui
l'etat vous demande de remboursé cette somme en 6ans cela fais 277.77e/mois
Donc si vous avez suivi vous allez payer 2 639,18 + 277.77 les 6 premieres années.
et les 19 derneire années seulement 2 639,18e
Le soucis 2639,18e + 277.77 c trop chere par mois
C la que le lissage rentre en jeux le but c diviser les 277.77e par mois sur les 25ans.
mais a savoir vous etes obligé de remboursé a l'etat cette somme en 6 ans.
donc vous allez emputé sur le remboursement du capital ce qui va conduire a une mensualité fixe pendant 25 ans.
Le lissage permet d'obtenir une mensualité fixe pendant toute la durée mais cela coute de l'argent donc cela n'est pas toujours interssant financierement.
Vous allez me dire 277e c rien par rapport à 2630 effectievement mais si le pret etait de 200 000e pour un foyé aux revenu moyen cela est ennorme.
Si une personne px m'aider a realisé ceci j'offirirai une recompense sympa :-)
Cordialement Christopher neuvy
Tel 06 82 96 08 39
Ps: j'adore les fautes d'orthographe ;-)
Lissage / emboitement de credit
15 messages
- Page 1 sur 1
par kazeriahm » 18 Mai 2007, 11:35
tu veux un algorithme qui te donne quoi?
j'ai pas tout suivi mais ca a l'air d'etre une succession de divisions non?
j'ai pas tout suivi mais ca a l'air d'etre une succession de divisions non?
par superloulou77 » 18 Mai 2007, 15:41
kazeriahm a écrit:tu veux un algorithme qui te donne quoi?
j'ai pas tout suivi mais ca a l'air d'etre une succession de divisions non?
C beaucoup plus compliqué
Voila un lien qui explique tres clairement en quoi cela consite.
http://www.cbanque.com/credit/lissage.php
Cordialement Christopher
par Quidam » 18 Mai 2007, 18:29
La formule magique est : ^{-n}})
Qui indique que pour rembourser en n périodes un capital emprunté au taux t par période, il faut n paiements à terme échu d'un montant de R.
Si j'ai bien compris ton problème, le prêt "prétendûment à 4%" est en fait un prêt à (4/12)% par mois (t=1/300) (ce qui est en fait un prêt à^{12}\ \ -1]*100)
% soit 4,074 % par an - désolé, je ne peux pas m'en empêcher ! Je ne peux pas supporter que les "prêteurs" continuent de parler d'un taux de 4% alors que c'est manifestement un taux de 4,074% !). Tu veux déterminer un montant mensuel R fixe pendant 25 ans (300 mois) qui rembourse d'une part le prêt à taux 0, d'autre part le prêt à (1/3)% par mois.
Soit a le remboursement du prêt à taux 0 (a=20000/72=277.77). Tout se passe comme si l'emprunteur avait fait deux emprunts. Un emprunt d'une somme C1 remboursée en 72 mois, une somme C2 (avec C=C1+C2=500000 ; les 20000 euros prêtés à taux 0 ne sont pas dans le coup, ils interviennent juste en diminuant de a le remboursement du prêt payant pendant 72 mois) non remboursée pendant 72 mois (ce qui signifie qu'avec les intérêts, C2 a augmenté !).
Pendant 72 mois, la somme C1 est remboursée avec la mensualité R-a. Donc :
^{-72}}\ \ \ [1])
Pendant ces 72 mois, C2 a augmenté pour devenir^{72})
. A partir de la fin de ce 72-ième mois, on rembourse la somme due (^{72})
) par 19*12=228 mensualité d'un montant de R, donc :
^{72}\ t}{1-(1+t)^{-228}}\ \ \ [2])
On retourne les formules [1] et [2] comme des chaussettes :
^{-72}))
^{72}(1-(1+t)^{-228}))
Et comme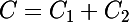
:
^{-72})+\frac{R}{t}(1+t)^{72}(1-(1+t)^{-228}))
Tu connais tout dans cette formule : la seule inconnue, c'est R. C'est une équation du premier degré à une inconnue... D'où R=...
Qui indique que pour rembourser en n périodes un capital emprunté au taux t par période, il faut n paiements à terme échu d'un montant de R.
Si j'ai bien compris ton problème, le prêt "prétendûment à 4%" est en fait un prêt à (4/12)% par mois (t=1/300) (ce qui est en fait un prêt à
Soit a le remboursement du prêt à taux 0 (a=20000/72=277.77). Tout se passe comme si l'emprunteur avait fait deux emprunts. Un emprunt d'une somme C1 remboursée en 72 mois, une somme C2 (avec C=C1+C2=500000 ; les 20000 euros prêtés à taux 0 ne sont pas dans le coup, ils interviennent juste en diminuant de a le remboursement du prêt payant pendant 72 mois) non remboursée pendant 72 mois (ce qui signifie qu'avec les intérêts, C2 a augmenté !).
Pendant 72 mois, la somme C1 est remboursée avec la mensualité R-a. Donc :
Pendant ces 72 mois, C2 a augmenté pour devenir
On retourne les formules [1] et [2] comme des chaussettes :
Et comme
Tu connais tout dans cette formule : la seule inconnue, c'est R. C'est une équation du premier degré à une inconnue... D'où R=...
par Quidam » 22 Mai 2007, 08:30
Désolé, j'ai fait une erreur. La formule finale du post précédent est erronée : la voici corrigée :
^{-72})+\frac{R}{t}(1+t)^{-72}(1-(1+t)^{-228}))
De là on termine par :
^{-72})+\frac{R}{t}((1+t)^{-72}-(1+t)^{-300}))
^{-72}) = R \times [\frac{1}{t}(1-(1+t)^{-72})+\frac{1}{t}((1+t)^{-72}-(1+t)^{-300})])
^{-72}) = R \times [\frac{1}{t}(1-(1+t)^{-300})])
^{-72}) }{\frac{1}{t}(1-(1+t)^{-300})}=\frac{Ct+a(1-(1+t)^{-72}) }{(1-(1+t)^{-300})})
De là on termine par :
par superloulou77 » 22 Mai 2007, 13:36
Merci c super cela fonction au centime d'euro pres.Je n'arrive pas a gerer des lissage avec differé. Px tu nous meme juste sur la route.car le pret a tx zero a des partcularité qui est le differé.
un pret a taux zero de 20 ans on doit remboursé 25% sur les 18 premiere année et les 75% restant pendant les 2 dernieres annees.
Et un pret classique px etre diffrée aussi.
Merci d'avance , cela est vraiment tres sympatique !!!!!! :++:
un pret a taux zero de 20 ans on doit remboursé 25% sur les 18 premiere année et les 75% restant pendant les 2 dernieres annees.
Et un pret classique px etre diffrée aussi.
Merci d'avance , cela est vraiment tres sympatique !!!!!! :++:
par Quidam » 22 Mai 2007, 20:07
superloulou77 a écrit:Merci c super cela fonction au centime d'euro pres.
Pas d'accord ! J'ai fait une simulation avec mon PC ! A condition de faire payer l'emprunteur : 2732.8981826227 euros chaque mois (et 277.77 de moins pendant les 72 premiers mois), le capital restant dû après 300 mois est évalué à 0.0000000181 euros, soit moins de 2 dix-millionnièmes de centimes d'euros. Evidemment, si tu fais payer un nombre entier de centimes chaque mois (2732,90) alors le capital restant dû sera -0.93 et quelques poussières, c'est-à-dire que l'emprunteur aura payé 93 centimes d'euros de trop ! Mais ça ce n'est pas mon problème !
superloulou77 a écrit:un pret a taux zero de 20 ans on doit remboursé 25% sur les 18 premiere année et les 75% restant pendant les 2 dernieres annees.
Facile ! A condition que tu précises car c'est ambigu : xxx.xx par mois pendant 18 ans et yyy.yy par mois pendant deux ans...
En fait, il est facile d'établir une formule générale liant C, R1, R2, R3,...Rn, mensualités respectives pendant k1 mois, pendant k2 mois...,..., pendant kn mois...
par superloulou77 » 23 Mai 2007, 14:49
Justement nous avons testé avec plusieurs prêts quelconques et cela fonctionne . Mais dans certain cas le prêt à taux zéro peut offrir un differé (prêt à pallier) comme par exemple :
La personne doit rembourser 0,75% du montant du prêt pendant les 18 premières années et 0,25% du montant pendant les 3 dernières années
Pour un montant de 11000e je dois rembourser 38,19 pendant les 18 premières années puis 76,39 pendant les 3 dernières années.
En utilisant ton équation et en admettant que le prêt à 0% peut être décomposer en 2 prêts (l'un de 18 ans avec une mensualité de 38,19 et le second sur 3 ans avec une mensualité de 76,39) on obtient une mensualité lissée qui n'est pas exacte (comparée avec d'autres logiciels de lissage).
Il semblerait que le lissage avec un prêt à taux zéro ayant un différé bénéficie d'un traitement spécial (la mensualité que j'ai calculée est supérieur à celle trouvée sur les autres logiciels de lissage).
Merci d'avance
La personne doit rembourser 0,75% du montant du prêt pendant les 18 premières années et 0,25% du montant pendant les 3 dernières années
Pour un montant de 11000e je dois rembourser 38,19 pendant les 18 premières années puis 76,39 pendant les 3 dernières années.
En utilisant ton équation et en admettant que le prêt à 0% peut être décomposer en 2 prêts (l'un de 18 ans avec une mensualité de 38,19 et le second sur 3 ans avec une mensualité de 76,39) on obtient une mensualité lissée qui n'est pas exacte (comparée avec d'autres logiciels de lissage).
Il semblerait que le lissage avec un prêt à taux zéro ayant un différé bénéficie d'un traitement spécial (la mensualité que j'ai calculée est supérieur à celle trouvée sur les autres logiciels de lissage).
Merci d'avance
par Quidam » 24 Mai 2007, 11:40
superloulou77 a écrit:Pour un montant de 11000e je dois rembourser 38,19 pendant les 18 premières années puis 76,39 pendant les 3 dernières années.
Ceci est équivalent au processus suivant. La mensualité R, fixe pendant toute la période de N années, rembourse les deux prêts. Pendant 18*12 mois, elle se décompose en 38,19 pour rembourser le prêt à taux 0, et (R-38,19) pour rembourser l'autre. Pendant 3*12 mois, elle se décompose en 76,39 pour rembourser le prêt à taux 0, et (R-76,39) pour rembourser l'autre. Et pendant le reste du temps (N-216-36 mois) elle est intégralement consacrée au remboursement de l'autre.
Tout se passe comme si tu devais :
Payer une mensualité
Payer une mensualité
Payer une mensualité
Je te donne le calcul général pour un prêt avec plusieurs mensualités différentes. Prenons le cas de 4 périodes.
Pendant
Pendant
Pendant
Pendant
Je rappelle la formule magique de base :
ou
Formule liant le capital C, la mensualité (ou annuité, ou...) R, le nombre de périodes n et le taux t (par période), d'un prêt.
En payant
En payant
Mais
Par conséquent :
ou
En payant
Mais
Par conséquent :
ou
En payant
Mais
Par conséquent :
ou
Or, à la fin, on est censé avoir tout remboursé. Il en résulte que :
et donc, que :
S'il y a trois périodes, et non quatre, la formule sera (il n'y a qu'à faire
Ton problème consiste à trouver R. Ici,
Donc l'équation devient :
ou
Et ceci est une équation du premier degré en R : facile !
par superloulou77 » 25 Mai 2007, 13:43
Super pour la formule pour le lissage a taux zero
Px tu nous la transformer en R= formule.
Car nous n'y arrivons pas.
Pour le teg voila la formule
http://www.cbanque.com/credit/teg2.php
Il me manque un élément afin de compléter ta formule : je ne sais pas comment inclure le coût mensuel des assurances dans la variable "tm" et donc trouver "tA" :/
Merdi d'avance. Christopher
ps : regarde tes messages privée
Px tu nous la transformer en R= formule.
Car nous n'y arrivons pas.
Pour le teg voila la formule
http://www.cbanque.com/credit/teg2.php
Il me manque un élément afin de compléter ta formule : je ne sais pas comment inclure le coût mensuel des assurances dans la variable "tm" et donc trouver "tA" :/
Merdi d'avance. Christopher
ps : regarde tes messages privée
par pi-phi2 » 18 Mar 2014, 21:19
salut.
je suis peut-être en retard de plusieurs années vu la date du post précédent .
parce que j'ai cherché et trouver une formule pour avoir directement la mensualité lissée avec le prêt principal lisseur à condition que le tout soit lissable. mais je pense que cette formule doit être connue depuis ces dernières années.
je suis peut-être en retard de plusieurs années vu la date du post précédent .
parce que j'ai cherché et trouver une formule pour avoir directement la mensualité lissée avec le prêt principal lisseur à condition que le tout soit lissable. mais je pense que cette formule doit être connue depuis ces dernières années.
par floarnaud » 26 Mar 2014, 12:33
bonjour,
je suis surement aussi en retard, mais ta formule pourrait m'interesser
merci d'avance
je suis surement aussi en retard, mais ta formule pourrait m'interesser
merci d'avance
Formule inversée et généralisée de Quidam
par faidherbard » 14 Mai 2014, 18:39
Grâce au message de Quidam qui date de 2007, voici la formule inversée et généralisée pour tous ceux qui la cherchent encore :
^{-N}}\;+\;a_1\,\times\,\frac{1-(1+t)^{-n_1}}{1-(1+t)^{-N}}\;+\;a_2(1+t)^{-n_1}\,\times\,\frac{1-(1+t)^{-n_2}}{1-(1+t)^{-N}}\;+\;a_3(1+t)^{-n_1-n_2}\,\times\,\frac{1-(1+t)^{-n_3}}{1-(1+t)^{-N}}\;+\;\dots)
Où :
Où :
est le remboursement pendant la période
pendant
pendant
- ...
par faidherbard » 14 Mai 2014, 19:19
Et pour superloulou77 qui posait la question de l'ajout du coût mensuel des assurances, c'est très simple :
Où
est le taux mensuel de l'assurance.
Où
par pi-phi2 » 14 Mai 2014, 20:34
salut.
et pour les prêts différés la formule telle quelle ne peut être appliquée . alors voici la formule générale .
en sachant que : C est le prêt principal. t , son taux mensuel proportionnel & z , sa durée.
si , avec ce prêt principal lisseur , on emboite n prêts secondaires remboursables sur m mois dont certains comme le PTZ peuvent être différés d'une durée d mois .
en sachant aussi que si le différé est nul , il suffit d'affecter l'exposant -d de la valeur 0 , le polynôme^0 = 1)
^{-d_i}}\times{\left[1 - (1+t)^{-m_i}\right]}}}{1 - (1+t)^{-z}})
tout cela est très linéaire puisque chaque mensualité de prêt secondaire n'est formulé qu'avec son différé , sa durée et le taux mensuel du prêt principal.
Une autre façon d'écrire cette mensualité lissée avec M , la mensualité du prêt principal seul .
pour 26 prêts lissés dans ce cas.
a plus. j.p.p
et pour les prêts différés la formule telle quelle ne peut être appliquée . alors voici la formule générale .
en sachant que : C est le prêt principal. t , son taux mensuel proportionnel & z , sa durée.
si , avec ce prêt principal lisseur , on emboite n prêts secondaires remboursables sur m mois dont certains comme le PTZ peuvent être différés d'une durée d mois .
en sachant aussi que si le différé est nul , il suffit d'affecter l'exposant -d de la valeur 0 , le polynôme
tout cela est très linéaire puisque chaque mensualité de prêt secondaire n'est formulé qu'avec son différé , sa durée et le taux mensuel du prêt principal.
Une autre façon d'écrire cette mensualité lissée avec M , la mensualité du prêt principal seul .
a plus. j.p.p
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :