Linéarité / Bilinéarité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 26 Nov 2007, 11:36
par barbu23 » 26 Nov 2007, 11:36
Bonjour :

et biniléaire et

est linéaire.
Pourquoi

est bilinéaire ?
Merci d'avance !!
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 26 Nov 2007, 12:03
par yos » 26 Nov 2007, 12:03
Salut.
Si tu explicites les ensembles de départ et d'arrivée de tout le monde, tu auras fait le plus gros du travail.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 26 Nov 2007, 12:08
par barbu23 » 26 Nov 2007, 12:08
Salut "yos" :
Voiçi le problème de depart :
Je note

l'application définie de
 \times L(E,F \times G)$)
dans
 $)
par
 \mapsto u \circ v$)
.

est bilinéaire.
Pourquoi

est bilinéaire ? ici :

est bilinéaire ! donc

c'est pas bilineaire !car il faut que :

soit linéaire pour pouvoir deduire ! je comprends pas !
Merci infiniment !!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 26 Nov 2007, 12:50
par barbu23 » 26 Nov 2007, 12:50
Salut "legeniedesalpages" :
ça fait longtemps que je t'ai pas vu ! :lol2:
Tu peux stp m'aider sur ce problème !
Merci infiniment !
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 26 Nov 2007, 13:11
par yos » 26 Nov 2007, 13:11
La bilinéarité de

n'a aucun rapport avec celle de u ou de v. Elle provient de la structure d'ev de l'ensemble de départ.
On a
\circ v=u\circ v+u'\circ v)
et pareil avec ku. C'est la linéarité à gauche.
 par legeniedesalpages » 26 Nov 2007, 13:15
par legeniedesalpages » 26 Nov 2007, 13:15
salut

tu veux montrer que
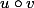
est bilinéaire ou que

est bilinéaire?
De toute façon, pour montrer qu'une application est bilinéaire, il me semble que c'est souvent cette méthode: vérifier la définition d'une application bilinéaire

point par point:
\qquad f(x_1+x_2,y) = f(x_1,y)+f(x_2,y),)
\qquad f(\lambda x, y)=\lambda f(x,y),)
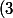\qquad f(x,y_1+y_2)=f(x,y_1)+f(x,y_2),)
\qquad f(x,\mu y) = \mu f(x,y))
quels que soient
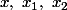
dans

,
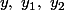
dans

et
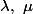
dans le corps

.
Sinon tu peux peut-être vérifier que ton application est linéaire par rapport à chacune de ses variables.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 26 Nov 2007, 15:53
par barbu23 » 26 Nov 2007, 15:53
Oui, mais pourquoi :
 = u \circ v_{1} + u \circ v_{2} $)
c'est ça ce que je coprends pas !

$ est bilinéaire ! ça donne le même resultat !!?
Merci d'avance de votre aide !
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 26 Nov 2007, 17:51
par yos » 26 Nov 2007, 17:51
Ah oui t'as raison : la linéarité à droite nécessite la linéarité de u. J'ai regardé un peu vite. Mais pour la linéarité à gauche, c'est la définition de la somme de deux applications (et du produit externe).
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 15 invités