Linearité et anti linéaire

[bSylvain]

Bonjour,

Je souhaite montrer que la forme (1) ci-dessous est linéaire à partir de la définition (2)

(1) ;)(x,y)=ix2y1* + iy2x1* ; E=C2 ; notera x=(x1,x2) où x1 et x2 sont des complexes

(2) ;)(;)x+y,z) = ;);)(x,z) + ;)(y,z) ; linéaire p/r à x

Je n'arrive pas à appliquer la définition (2) à la relation (1)

Merci beaucoup de votre aide

bSylvain

[Robot]

(1) est la définition de .
(2) n'est pas une définition : c'est une propriété vérifiée (ou non) par l'application .

Pourquoi ne continues pas dans cette discussion ?

Je ne comprends pas ce qui t'empêche, dans la définition de (le (1)) de remplacer par et par ?

[bSylvain]

Pouvez vous svp m aider à montrer que c est linéaire à partir de la propriété ?
Merci d avance.
Bsylvain

(1) est la définition de .
(2) n'est pas une définition : c'est une propriété vérifiée (ou non) par l'application .

Pourquoi ne continues pas dans cette discussion ?

Je ne comprends pas ce qui t'empêche, dans la définition de (le (1)) de remplacer par et par ?

[Robot]

Qu'est-ce qui te dit que c'est linéaire ?

Je ne comprends pas ton obstination à ne rien faire. La route à suivre est pourtant claire :
1° Calculer (le membre de gauche de l'égalité dans (2)), en utilisant la définition de (le (1)).
2° Calculer (le membre de droite de l'égalité dans (2)) en utilisant la définition de \varphi (le (1)).
3° Décider si on obtient le même résultat ou des résultats différents.

C'est plus facile que de monter un meuble IKEA ! :lol3:

Allez, je commence avec un petit bout du 2° : on voit dans le membre de droite . D'après la définition de i, on a

(dans la définition de , on remplace la lettre par la lettre et la lettre par la lettre ).

Je te laisse continuer.

[paquito]

Une fois n'est pas coutume, je suis presque entièrement d'accord avec Robot, sauf pour IKEA: ce qui est facile, c'est de rentrer dans le magasin, mais ce qui peut rendre fou, c'est de vouloir sortir de ce labyrinthe diabolique. :ptdr:
Quant à ton exercice, Robot t'a dit à juste titre que c'était élémentaire.
Par contre, c'est quoi, antilinéaire??? Un altermondialiste qui ne veut pas aller tout droit sachant qu'il va se planter forcément ou une erreur de la nature ou ...
Mystère! :mur:

[Robot]

je suis presque entièrement d'accord avec Robot, sauf pour IKEA

Tu n'es donc pas d'accord avec le fait que l'exercice est plus simple que le montage d'un meuble IKEA ?

Par contre, c'est quoi, antilinéaire???

On dit plutôt "semi-linaire". Voir cette page wikipedia.

Ah au fait, paquito, tu n'avais pas précisé si tu enseignais bien l'utilisation des quaternions pour la manipulation des rotations de l'espace ?

[paquito]

Tu n'es donc pas d'accord avec le fait que l'exercice est plus simple que le montage d'un meuble IKEA ?

On dit plutôt "semi-linaire". Voir cette page wikipedia.

Ah au fait, paquito, tu n'avais pas précisé si tu enseignais bien l'utilisation des quaternions pour la manipulation des rotations de l'espace ?

Comme toujours, il te faut une bombe H pour supprimer une drosophile qui squate la touche µ de ton PC! :pirate:

En ce qui concerne le montage d'un "meuble" en kit, essaie de monter un bureau d'ordinateur avec tour et plateau coulissant pour le clavier, en aluminium et verre opaque acheté une misère à conforama; si au bout de 5 h de prise de tête, tu n'as pas des envies de meurtres, c'est que le niveau de ton self control doit te permettre de rentrer dans le Guiness des records! :ptdr:

Sinon, moi aussi, je préfère semi linéaire; c'est quand même mieux que d'essayer de faire un truc avec du vide! :lol3:

[Robot]

Comme toujours, il te faut une bombe H pour supprimer une drosophile qui squate la touche µ de ton PC!

Je ne comprends pas. A quoi fais-tu allusion ?

[paquito]

Je ne comprends pas. A quoi fais-tu allusion ?

c'est comme utiliser le fait que C soit algébriquement clos pour démontrer que admet exactement une racine!

Petit conseil amical: Tu vas trop souvent te promener dans un magasin IKEA; si en plus tu fais ta déco personnelle en IKEA, en fait tu cherches la corde pour te pendre; si tu veux te détendre un peu on trouve facilement des casse tête très décoratifs en bois ou pour varier un peu un puzzle de 10000 pièces représentant un champ recouvert de neige! :mur: :karate: :zen:

[Robot]

Bon, tu réponds à côté. Enfin, inutile de polluer plus longtemps ce fil. Voyons si bSylvain s'en sort.

[bSylvain]

Merci Robot pour ton aide,
Il est clair que la forme explicite de \varphi. n'est pas linéaire par rapport à premiere variable x
Il est clair également qu’elle n'est anti-linéaire (semi linéaire - je n'aime pas cette terminologie ) par rapport à la deuxième variable y de \varphi.

Robot comme tu as pu le lire ailleurs je suis en reprise d'études ce qui n'est pas facile, je bloque sur des choses élémentaires. Merci encore de l'aide!

---------------

Je vais laissé le petit problème ci-dessous pour paquito, qui est toujours plus simple que chez IKEA !
Est ce que forme un produit scalaire dans un espace de Hilbert?
E=Rn[X] (P,Q)=;);)P(k)Q(k);); k=0 à n

bSylvain

Bon, tu réponds à côté. Enfin, inutile de polluer plus longtemps ce fil. Voyons si bSylvain s'en sort.

[paquito]

Prière d'utiliser les balises TEX STP.

n'est pas un produit scalaire. De plus tu aurais dû écrire dans cet espace de Hilbert et non pas dans un espace de Hilbert.

Précision: si n=0, ça marche quand même, mais dès que n =1 tu obtiens des exemples ou , ce qui est gênant pour un carré scalaire!

PS: C'est quand même beaucoup moins stressant que le "jeu de piste" dans un labyrinthe que tu subiras si par pure ignorance tu pénètre dans un magasin IKEA. Quant à monter un "meuble en kit de chez eux, c'est assimilable à une longue séance de torture condamnée par amnesty international! :lol3:

[Robot]

n'est pas un produit scalaire. De plus tu aurais dû écrire dans cet espace de Hilbert et non pas dans un espace de Hilbert.
Précision: si n=0, ça marche quand même, mais dès que n =1 tu obtiens des exemples ou , ce qui est gênant pour un carré scalaire!

est bien sûr un produit scalaire, et munit d'une structure d'espace euclidien.
C'est évidemment une forme bilinéaire symétrique.
Par dur de voir qu'elle est définie positive.

[bSylvain]

Je confirme c'est bien un produit scalaire.

têta satisfait trivialement toutes les propriétés d'un produit scalaire.


Paquito, essaye du coté ou P=Q :lol3:

Est ce plus dur qu'un problème de chez Ikea? attention à la tête le mur est plus dur.

Je prend mes études apres 20ans, j'ai gratté du meuble mais de chez IKEA...

[bSylvain]

J’arrête de faire le rigolo car quand j'étais sec (j'ose le dire) sur une simple linéarité (qui d'ailleurs le n'était pas)

Merci à vous

[paquito]

Je suppose que je n'ai rien compris aux notations de bSylvain. si 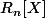désigne l'E.V. des polynômes d'une variable de degré au plus n, dans ce cas, effectivement est bien une forme bilinéaire symétrique définie positive; ce qui confirme, s'il le fallait, vos conclusions.
Désolé d'avoir semé un léger trouble dans la discussion!
Faut dire que j'ai été piégé par IKEA hier après midi, ce qui me donne des circonstances atténuantes!
:lol3: :--:

[bSylvain]

Je suppose que je n'ai rien compris aux notations de bSylvain. si désigne l'E.V. des polynômes d'une variable de degré au plus n, dans ce cas, effectivement est bien une forme bilinéaire symétrique définie positive; ce qui confirme, s'il le fallait, vos conclusions.
Désolé d'avoir semé un léger trouble dans la discussion!
Faut dire que j'ai été piégé par IKEA hier après midi, ce qui me donne des circonstances atténuantes!
:lol3: :--:

Merci a vous de votre aide.
Je reviendrai surement par ici, la je suis dans les espaces de sobolev dans le cadre la formulation variationnelle du problème aux limites.

A bientot :lol3: