Limte difficile à atteindre à deux variables

[frankyboy1994]

Bonjour! Je n'arrive pas à résoudre cette limite, merci de bien vouloir m'aider:



Avec le graphique en 3D on voit bien que la limite est égale à 2.

[Ben314]

Salut,
Dire que "(x,y)->(0,0)", ça veut dire (par définition) que tend vers 0 (par contre sans aucune hypothèse concernant la/les directions avec lesquelles on s'approche de (0,0) ).
Donc ta limite est complètement équivalente à cas dans lequel... il y a plusieurs méthodes...

[frankyboy1994]

Dans mon cours de calcul, le prof nous dit qu'il faut essayer plusieurs "chemins", car dans le plan, contrairement à sur la droite où il n'y a que 2 chemins, il y une infinité de "chemins" possibles. Il faut donc poser par exemple x=0, y=0, y=x, y=x² etc. Si tous les chemins ne donnent pas la même valeur, alors la limite n'existe pas. Si tous les chemins donnent la même valeur, alors on pose la conjecture: et il faut prouver que: pour pouvoir dire que la conjecture est vraie. C'est la méthode que le prof nous a donnée donc sais-tu comment l'évaluer avec cette technique?

[Archibald]

Bonjour,

j'ai beaucoup plus simple : faire disparaître le radical en multipliant et divisant par son conjugué (même méthode qu'à une indéterminée), une identité remarquable apparaît et hop on simplifie. C'est ce qui devrait directement te venir à l'esprit avec une fonction de cette forme.





, d'où limite de f ...


La méthode de ton prof est classique, elle aide l'élève à faire la transition droite/plan, mais elle reste trop générale.

[arnaud32]

poses comme indique par ben.
ensuite tu utilises la quante conjuguee

[Ben314]

Ou alors tu dit que où ce qui revient (sans le dire) à utiliser la méthode de je sais plus qui consiste à lever les indéterminations 0/0 en dérivant numérateur et dénominateur.
Tu peut aussi faire un développement limité à l'ordre 1 de \sqrt{1+t} (çe qui est de nouveau exactement la même méthode vue sous un autre angle...) ou bien, comme l'ont fait Archibald et Arnaud, multiplier par la "quantité conjugué" ou bien ... (il y a surement d'autre façons de présenter...)

Je pense que de toute façon, ce qu'il faut absolument comprendre dans cet exercice, c'est que vu que ta fonction est de la forme (trés particulière) , où est une bète fonction réelle, ce qu'on te demande n'est pas une "vraie" limite dans 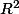, mais plutôt une limite réelle.
Ca signifie que, quelque soit la méthode employée, ça sera assez "spécial" par rapport aux méthode généralement employées pour les "vraies" fonctions de deux variables (où il faut quasi systématiquement utiliser des majorations)

[Ben314]

Aprés, concernant précisément ta question :

...il faut prouver que: pour pouvoir dire que la conjecture est vraie. C'est la méthode que le prof nous a donnée donc sais-tu comment l'évaluer avec cette technique?

oui, je sais comment l'évaluer : ... :zen:

[frankyboy1994]

Wow merci pour toutes ces réponses! Mais celle que je préfère est la technique de la multiplication par le conjugué sans changement de variable, parce que malheureusement mon expérience mathématique ne me permet pas encore, Ben, de voir avec facilité que est équivalente à (Je suis seulement à ma deuxième année de Cégep) Et dans un examen, j'ai besoin de rapidité! Par contre ça m'a appris que cette technique existe! Souvent je bûche sur un problème et j'oublie que la solution consiste en une simple transformation algébrique...

[Ben314]

...ne me permet pas encore, Ben, de voir avec facilité que...

Justement, ce que j'essaye de te faire comprendre, c'est que c'est la définition même de qui te dit que dans le cas où , il n'y a qu'à étudier .
Cette définition te dit :

Donc elle dit que faire tendre (x,y) vers (0,0), par définition, ça veut dire faire tendre vers 0...
Donc je trouve ça pas futé de chercher midi à 14 heures là où... il n'y a besoin de rien d'autre que de la définition...
Mais après, effectivement, pourquoi faire simple quand on peut faire compliqué ?

[frankyboy1994]

Ok, donc en résumé, si on peut trouver une fonction qui est une composée de et qui est égale à , on trouve la limite de et puisque, la limite de est égale à la limite de ? Mais pourquoi transformer en s'il faudra tout de même avoir recours à la technique du conjugué?

[Ben314]

...si on peut trouver une fonction qui est une composée de et qui est égale à ...

Ca, c'est trés mal formulée : il faut écrire "si on peut écrire f sous la forme de la composée d'une fonction réelle et de la fonction alors..."

Mais pourquoi transformer en s'il faudra tout de même avoir recours à la technique du conjugué?

Parce que on connait beaucoup beaucuop plus de méthode pour calculer des limites de fonctions réelles (i.e. de R->R) que de méthode pour calculer celles de R²->R.
Par exemple, dans le cas particulier présent, je vois au moins 3 méthodes pour calculer la limite de : quantité conjuguée ; développement limités ; faire apparaitre un calul de dérivée.
Sur ces 3 méthodes, UNE SEULE peut s'appliquer directement sur la fonction f, celle passant par le conjugué.

De plus, dans le cas où la fonction f n'est pas de la forme , la méthode pour calculer la limite de f consiste quasi systématiquement à majorer par une fonction ne dépendant que de x^2+y^2 et pas d'autre chose. donc ça signifie à mon sens que ces fameuses fonctions de la forme sont en général la "clef" pour trouver les limites de fonctions de plusieurs variables.

Tu verra que, dans les exercices un peu difficiles de ce type, ce qu'on fait trés fréquement, c'est de poser et puis de chercher à majorer par un truc qui ne dépend que de et pas de .
Si tu réfléchis 15 secondes, vu que , ce que tu fait dans ce cas là, ben c'est trés exactement d'essayer de majorer par un truc du style ...

[frankyboy1994]

D'accord, c'est donc parce qu'il y beaucoup plus de manières de calculer une limite à une variable que de manières de calculer une limite à plusieurs variables qu'on fait le changement de variable. Et ce que tu dis à la fin de ton message, c'est de faire un changement de variable en polaire? Merci encore!