lim
x->0
et
lim
x->+oo
Merci !
Limites
10 messages
- Page 1 sur 1
par fatal_error » 19 Sep 2009, 17:33
salut,
Pour la premiere, tu peux multiplier par les quantités conjuguées.
Pour la seconde,
est négligeable devant 
et 
devant 
en 
, puis par puissance comparées (jcrois que ca se dit comme ca je sais plus), en comparant et
Pour la premiere, tu peux multiplier par les quantités conjuguées.
Pour la seconde,
la vie est une fête 
par Laurent Porre » 19 Sep 2009, 17:48
|z| a écrit:Mais pour la première limite, je me retrouve avec un +oo/+oo ...
tu devrais avoir "1" au numérateur après avoir utilisé le conjugué, refais ton calcul
par |z| » 19 Sep 2009, 17:52
Mais bien sûr! Ne me demandez pas comment je me suis trompé, j'ai honte. :briques:
par |z| » 22 Sep 2009, 15:45
Désolé de vous importuner encore, j'ai de nouveau quelques petits soucis ...
Pouvez -vous m'indiquer où est mon erreur ?
Donc pour trouver:
lim/(x-3))^x)
x->+oo
Je passe au ln, méthode habituelle... Je transforme ensuite la fraction en/(1-3/x))
... Puis /(1-3/x))+1-1)
pour pouvoir appliquer les formules des équivalents... Mais vu que c'est en +oo et que les formules sont en O, je m'embrouille un peu... Est-ce que :
/(x-3)))
équiv.(0) /(1-3/x))-1)
? Et comme la fraction "-1" tend vers 1, mon résultat final serait 
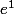
, soit 
? Or, maple m'indique 
comme solution...
Deuxième chose, j'ai besoin d'aide pour l'horrible limite suivante:
lim^2+(1/(x+1)) ) - sqrt(e)) / (ln(x+1) - ln(2)))
...
x->1
Désolé pour le format... Tout le "^2+(1/(x+1)) ))
" est à la puissance du e.
Merci bien.
Pouvez -vous m'indiquer où est mon erreur ?
Donc pour trouver:
lim
x->+oo
Je passe au ln, méthode habituelle... Je transforme ensuite la fraction en
Deuxième chose, j'ai besoin d'aide pour l'horrible limite suivante:
lim
x->1
Désolé pour le format... Tout le "
Merci bien.
par Laurent Porre » 22 Sep 2009, 16:36
tu as
/(x-3)))
= /(1-3/x)))
= - ln(1-3/x)))
or ln(1+x) ~ x (en 0)
donc ln (1+1/x) ~ 1/x (en +oo)
soit ~ x * (1/x - (-3/x)) = x * 4/X = 4
tu passes à l'exponentielle et tu as la limite e^4
pour la 2e, j'ai la flemme
=
or ln(1+x) ~ x (en 0)
donc ln (1+1/x) ~ 1/x (en +oo)
soit
tu passes à l'exponentielle et tu as la limite e^4
pour la 2e, j'ai la flemme
par |z| » 22 Sep 2009, 16:49
Laurent Porre a écrit:
Merci pour la réponse... Mais quelque chose me chagrine dans ton raisonnement: n'additionnes tu pas des équivalents ?
par Laurent Porre » 22 Sep 2009, 17:12
|z| a écrit:Merci pour la réponse... Mais quelque chose me chagrine dans ton raisonnement: n'additionnes tu pas des équivalents ?
tu as raison on additionne pas les équivalents en général, j'ai du aller un peu vite en besogne, hum ...
edit -> ah si on peut sommer des DL du même ordre, enfin je suis quasi sur donc c'est bon. De toute façon le calcul s'enchaine tellement bien que ça ne peut qu'être bon
par |z| » 22 Sep 2009, 17:23
Oui, merci... Je pense que "on ne peut pas additionner des équivalents" est vraie... Ce qui ne veut pas dire que l'on ne puisse pas parfois. :ptdr:
Edit: qui a le courage de m'aider pour la deuxième ? :happy2:
Edit: qui a le courage de m'aider pour la deuxième ? :happy2:
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :