Limites

[Vitlia]

Bonjour,
Je suis bloqué dans l'étude d'une fonction.
Il s'agit de la fonction f(x)=ln((x-2)/(lxl-4)) définie sur ]-4;2[U]4;+infini[.
Lorsque l'on étudie sa limite pour x qui tend vers +infini on se retrouve avec une forme indéterminée du type infini/infini. Les conditions étant réunies pour appliquer le théorème de l'Hopital, j'ai essayé de me reconduire à une fonction du type g'(x)/h'(x) pour trouver la limite. Cependant suite à la dérivation on se retrouve encore avec une forme indéterminée du même type que la précédente. Je pourrais dérivée à nouveau mais la fonction signe de x se trouvant au dénominateur je ne peux pas dérivée à nouveau car cette fonction n'a pas de dérivée. Comment faire ??
Merci d'avance pour votre aide.

[Ben314]

Salut,
une petite remarque "bébète" : lorsque tu t’intéresse à la limite lorsque x tend vers +oo, il me semble raisonable de considérer que x est positif...
(et il n'y a pas vraiment besoin de la règle de l’hôpital pour déterminer la limite)

[deltab]

Bonsoir.

L'utilisation de la règle de L'Hôpital ne donne pas de forme indéterminée !!!!! et elle est inutile si l'on connaît les croissances comparées entre les fonctions logarithme et les fonctions puissances.

[Vitlia]

Tout d'abord merci pour vos réponses ! :)
Deltab, je ne comprends pas pourquoi la règle de l'Hopital ne peut pas donner de forme indertéminée ??
Par exemple si on étudie la fonction suivante pour x qui tend vers 0:
F(x)=[(e^x)(e^(sin x))]\(x^3)
On se retrouve avec une forme indéterminée de la forme 0/0.
Mais en dérivant une 1ere et une 2nde fois on se retrouve de nouveau avec la même forme indéterminée.
C'est en dérivant une 3ème fois qu'on s'aperçoit que la limite de f(x) pour x qui tend vers 0 est de 1/6.
Alors ici en appliquant les deux premières fois la règle de l'hopital on retrouve une forme indéterminée.

Ai-je mal compris ?

:)

[Ben314]

Je me demande si deltab (et moi...) avons bien lu ton énoncé.
Vu les parenthèse que tu met, moi j'ai lu (et ça colle avec ton domaine de définition).
Donc ma remarque et celle de deltab allaient dans le sens que, pour calculer la limite en +oo de , il n'y avait pas vraiment besoin de sortir la règle de l'hopital : comme x>0 la valeur absolue s'en va et on a affaire à deux bête polynômes de même degrés qui se comportent comme leur termes de plus haut degré.
La limite de la fraction est donc 1 et la limite de f est ln(1)=0.

Aprés, là ou tu as raison, c'est qu'il y a des cas où la règle de l’hôpital ne s'applique pas directement, mais je pense que deltab parlait du cas précis de ton énoncé et pas "en général"

[Vitlia]

Oui oui vous avez très bien lu :)
Ben314 je te remercie pour les précisions !
Encore merci !!

[Archibald]

Par exemple si on étudie la fonction suivante pour x qui tend vers 0:
F(x)=[(e^x)(e^(sin x))]\(x^3)
On se retrouve avec une forme indéterminée de la forme 0/0.

ce n'est pas une F.I de la forme 0/0, la limite du numérateur au voisinage de 0 vaut 1

[deltab]

Bonsoir

Oui oui vous avez très bien lu
Ben314 je te remercie pour les précisions !
Encore merci !!

Vtilia, quant tu as parlé de la règle de L'Hôpital, j'ai alors fait une erreur de lecture, l'expression était bien parenthésée, j'ai vu la forme indéterminée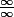 et j'avais lu et ma remarque concernant la règle de l'Hôpital ne donne pas de FI ne concernait que la fonction que j'avais lue (d'où la croissance comparée .......)