Limites et intégrales...
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Ludo1be
- Membre Relatif
- Messages: 220
- Enregistré le: 20 Juil 2009, 09:11
-
 par Ludo1be » 20 Juil 2009, 09:19
par Ludo1be » 20 Juil 2009, 09:19
Bonjour,
Je suis Belge, je rentre à l'université en sciences informatiques en septembre.
Je me suis muni des fiches de révision avec notamment ces derniers exercices qui me donnent du fil à retordre... Les voici:
Cette limite

Ces deux intégrales:

(Je sais juste intégrer par substitution et par parties)
Une aide surtout pour comprendre le raisonnement me serait de très grande utilité!!!
Bonne journée
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 20 Juil 2009, 09:41
par girdav » 20 Juil 2009, 09:41
Bonjour.
Pour le premier exercice: on fait une manipulation classique: multiplier par la quantité conjuguée. L'intérêt est que le dénominateur admet une limite finie et que le numérateur a une expression plus maniable.
Pour le deuxième: la première chose à faire est une décomposition en éléments simples (car on ne voit pas de truc évident genre

même si on bricole).*On cherche les coeffients qui satisfont à l'égalité
pour tout 
où le quotient ne s'annule pas (en fait en multipliant par un facteur bien choisi on va aussi prendre des valeurs où la fraction n'est pas définie). Comme
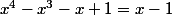^2\(x^2+x+1\))
alors cette décomposition est sous la forme indiquée.
Pour trouver
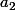
on multiplie par
^2)
et on remplace par

par

.
Après on remplace par d'autres valeurs pour trouver les autres coefficients.
Pour la dernière intégrale et la deuxième égalité, on coupe le dénominateur en deux: la première partie vaut
)
et l'autre donne de l'arctangente avec un peu de bricolage.
-
Ludo1be
- Membre Relatif
- Messages: 220
- Enregistré le: 20 Juil 2009, 09:11
-
 par Ludo1be » 20 Juil 2009, 10:08
par Ludo1be » 20 Juil 2009, 10:08
Tout d'abord, merci pour cette réponse rapide.
Pour le premier, on multiplie par la quantité conjuguée, OK. Ensuite, je lâche un peu... On dirait que toutes les racines sont levées au numérateur? Ensuite comment est-ce que cela peut passer à 2x - 1 ? J'ai vraiment pas saisi sur ce coup là...
Pour le second, j'ai tout compris, merci à toi ;-)
Pour le troisième, à vrai dire c'est la première fois que je dois calculer une intégrale avec égalité O_o Ce que j'ai vu durant mon cours de math cette année, c'était du calcul d'aire, des primitives, calculer des intégrales avec substitution et par parties, c'est tout...
A celle-ci, je suis totalement largué, je vois pas comment le 2 peux valoir 5/x-1 idem pour l'autre égalité... Quel est le raisonnement utilisé pour obtenir ceci?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 20 Juil 2009, 10:24
par girdav » 20 Juil 2009, 10:24
Tu dois penser trop compliqué pour la première: c'est tout simplement
\(a+b\))
.
Pour les intégrales: on cherche une primitive de la fonction constante égale à

, c'est-à-dire une fonction donc la dérivée vaut

. Il se trouve que
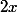
fait l'affaire.
Pour la deuxième, on doit avoir du logarithme puisque sa dérivée est
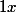
mais il faut que l'argument dedans soit strictement positif pour que ça ait un sens, d'où la présence de la valeur absolue.
-
Ludo1be
- Membre Relatif
- Messages: 220
- Enregistré le: 20 Juil 2009, 09:11
-
 par Ludo1be » 20 Juil 2009, 10:48
par Ludo1be » 20 Juil 2009, 10:48
Pour la première, oui, j'avais remarqué ce binôme conjugué mais c'est juste après où ce que ça ne va plus du tout... J'aimerais si ça ne te dérange pas que tu m'expliques en détail comment ce résultat a été obtenu.
Le premier exercice sur les intégrales, j'ai bien tout compris maintenant (je te remercie en passant).
Maintenant, pour le dernier, Waw O_o Ok, la dérivée de 2x = 2.
Mais comment arrive-t-on à obtenir 5/x-1 avec un 2... O_o j'ai du louper grave quelque chose sur ce coup... idem pour l'égalité... Surtout sur ce point que j'aimerais que l'on m'explique si possible...
Merci d'avance ;-)
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 20 Juil 2009, 11:10
par girdav » 20 Juil 2009, 11:10
On a:
^2} = \fr{\(\sqrt{x} - \sqrt{1-x}\)}{\(2x-1\)^2}\fr{\(\sqrt{x} +\sqrt{1-x}\)}{\(\sqrt{x} + \sqrt{1-x}\)}<br />= \fr{\sqrt{x}^2 - \sqrt{1-x}^2}{\(\sqrt{x} + \sqrt{1-x}\)\(2x-1\)^2}<br />= \fr{x-\(1-x\)}{\(\sqrt{x} + \sqrt{1-x}\)\(\(2x-1\)^2\)})
Après simplification du
)
on voit que la limite à gauche est différente de la limite à droite.
Pour

: tu regardes pour
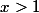
: en dérivant
)
tu arrives au résultat et pareil pour
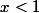
.
Pour la dernière:
 +2}{\(x+1\)^2+\fr{3}{4}}dx <br />=2\underbrace{\int{\fr{2x+1}{x^2+x+1}dx}}_{\ln(x^2+x+1\)}+ 2 \int\fr{dx}{\(\fr{3}{4}\)\(\(\fr{x+1}{\fr{\sqrt{3}}{2}}\)^2 +1\)})
-
Zavonen
- Membre Relatif
- Messages: 213
- Enregistré le: 23 Nov 2006, 10:32
-
 par Zavonen » 20 Juil 2009, 11:25
par Zavonen » 20 Juil 2009, 11:25
Nous apprenons quand même du corrigé 'officiel' du premier exercice que +

est un nombre et que -

en est un autre.
Instructif ...
-
Ludo1be
- Membre Relatif
- Messages: 220
- Enregistré le: 20 Juil 2009, 09:11
-
 par Ludo1be » 20 Juil 2009, 11:28
par Ludo1be » 20 Juil 2009, 11:28
Nickel pour la limite, j'ai enfin compris!
Pour la dernière intégrale... Ok, le premier terme est toujours égal à sa dérivée mais ça ne me dit toujours pas pourquoi on passe de 2 à 5/x-1 ...
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 20 Juil 2009, 11:34
par girdav » 20 Juil 2009, 11:34
Ce sont deux intégrales distinctes et on a mis directement le résultat pour les deux.
-
Ludo1be
- Membre Relatif
- Messages: 220
- Enregistré le: 20 Juil 2009, 09:11
-
 par Ludo1be » 20 Juil 2009, 12:07
par Ludo1be » 20 Juil 2009, 12:07
Ok, voila qui complique nettement moins les choses ;-)
Donc pour ce point 4:
La première, no soucy.
La seconde, également
La troisème, si j'integre par substitution, ça ne donne pas le même résultat normal?!!! J'arrive à 4 ln |x-1|²
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 20 Juil 2009, 12:09
par girdav » 20 Juil 2009, 12:09
Non, il faut dériver

. Là tu l'intègres de nouveau.
-
Ludo1be
- Membre Relatif
- Messages: 220
- Enregistré le: 20 Juil 2009, 09:11
-
 par Ludo1be » 20 Juil 2009, 12:15
par Ludo1be » 20 Juil 2009, 12:15
En fait, moi j'ai intégré 4/(x-1)²
Pourquoi est-ce que il arrive à [-4/x-1] ? Et pourquoi devoir dériver cela pour pouvoir intégrer par la suite?
D'après mon cours de math de cette année, la façon dont je procédais fut la bonne... Je ne comprends vraiment pas ce qui diffère ici
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 20 Juil 2009, 12:24
par girdav » 20 Juil 2009, 12:24
On a
^2} = 4\int\fr{1.dx}{\(x-1\)^2})
.
On reconnaît une forme

qui s'intègre en

(on vérifie le résultat en dérivant

avec le résultat sur les fonctions composées).
La dérivation permet de vérifier le résultat car on cherchait une fonction telle que sa dérivée soit égale à la fonction à intégrer.
-
Ludo1be
- Membre Relatif
- Messages: 220
- Enregistré le: 20 Juil 2009, 09:11
-
 par Ludo1be » 20 Juil 2009, 12:42
par Ludo1be » 20 Juil 2009, 12:42
Ha oui, ok, donc c'est une formule à part entière. En fait je l'ai remarquée au moment même où tu as posté ce message.
Ici dans mon cours j'ai par exemple
S 8x²/(x³-2)³
Dans ce cas-ci, nous avions utilisé la méthode d'intégration par substitution, ce qui nous donne au final -4/(x³+2)².3
Imaginons que le numérateur aurait été simplement 8, est-ce que dans ce cas là nous aurions pu utiliser cette formule?
En passant BIG merci gairdav ;-)
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 20 Juil 2009, 12:47
par girdav » 20 Juil 2009, 12:47
Dans ce cas-ci, nous avions utilisé la méthode d'intégration par substitution, ce qui nous donne au final -4/(x³+2)².3
Oui.
Imaginons que le numérateur aurait été simplement 8, est-ce que dans ce cas là nous aurions pu utiliser cette formule?
Non car on a plus
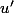
en haut: il faut donc recourir à la méthode de décomposition en éléments simples.
-
Ludo1be
- Membre Relatif
- Messages: 220
- Enregistré le: 20 Juil 2009, 09:11
-
 par Ludo1be » 20 Juil 2009, 13:47
par Ludo1be » 20 Juil 2009, 13:47
Ha ok, donc si j'ai bien compris afin d'utiliser cette formule il faut obligatoirement[B] que le numérateur soit la dérivé du dénominateur.
Maintenant, si j'ai:
S tgx dx Cela me fait donc S sin x/cos x
(Méthode par substitution : t = cos x
dt = -sin x
Donc, S - dt/t = - S 1/t
--> -ln(t) + C
Dans ce cas-ci faut-il appliquer cette formule ou non? Car dans mon énoncé précédent, c'était le 4 que je mettais hors de l'intégrale, et ici le - ...
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 20 Juil 2009, 15:56
par girdav » 20 Juil 2009, 15:56
Oui (en fait l'intégration par substitution est le changement de variable), c'est la bonne méthode. Mais il fait faire attention au signe de
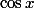
.
En fait on met ce qui nous "gêne".
-
Ludo1be
- Membre Relatif
- Messages: 220
- Enregistré le: 20 Juil 2009, 09:11
-
 par Ludo1be » 20 Juil 2009, 17:15
par Ludo1be » 20 Juil 2009, 17:15
Si j'applique cette formule à mon énoncé précédent, je n'ai vraiment pas le même résultat que avec la méthode de substitution, normal?... Or je peux l'appliquer puisque cela correspond bien à u'/u...
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 21 Juil 2009, 07:17
par girdav » 21 Juil 2009, 07:17
Ca correspond à

au signe près (c'est peut-être là que les résultats diffèrent).
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités


