Limites de fonctions

[xNiicO]

Bonjour,

Voulant m'exercer j'ai pu trouver deux limites que je cherche activement depuis plusieurs jours en testant les factorisations, multiplication par le conjugué, utilisation de dérivée mais rien à faire, je sèche complétement.

1)

2)

J'ai aussi une indication que j'ai testé mais j'ai pas trouvé l'utilité au final.

Indication : On pourra utiliser la notion de dérivée.

[Zine]

salut,

Pour la première ,
j'aurais fait la limite en 0

c'est à dire :

[Zine]

pour la 2 , utilise l'indication

avec a=0

[mrif]

Bonjour,

Voulant m'exercer j'ai pu trouver deux limites que je cherche activement depuis plusieurs jours en testant les factorisations, multiplication par le conjugué, utilisation de dérivée mais rien à faire, je sèche complétement.

1)

2)

J'ai aussi une indication que j'ai testé mais j'ai pas trouvé l'utilité au final.

Indication : On pourra utiliser la notion de dérivée.

1) tu écris la définition du nombre dérivée en -1 de la fonction f(x) = x^1000 + 2x + 1
2) ..........................................................0 ....................g(x) = e^(tan(x)) - 1

[arnaud32]

donc

[xNiicO]

1) tu écris la définition du nombre dérivée en -1 de la fonction f(x) = x^1000 + 2x + 1
2) ..........................................................0 ....................g(x) = e^(tan(x)) - 1

Quel est le but de faire ça ?

Pourquoi faire que le numérateur à chaque fois pour les nombres dérivées ?

donc

Je suis pas d'accord sur ta dernière expression car quand on développe on ne retrouve pas le membre de gauche Si je dis pas de bêtises il te manque juste un x en facteur sur tout le membre de droite

Donc une fois fait cela revient à étudier :



Donc :

et

Je me trompe ?

[busard_des_roseaux]

bonjour,
ton 1er quotient s'écrit

[arnaud32]

Quel est le but de faire ça ?

Pourquoi faire que le numérateur à chaque fois pour les nombres dérivées ?




Je suis pas d'accord sur ta dernière expression car quand on développe on ne retrouve pas le membre de gauche Si je dis pas de bêtises il te manque juste un x en facteur sur tout le membre de droite

Donc une fois fait cela revient à étudier :



Donc :

et

Je me trompe ?

oui tout a fait, faute de frappe


ceci dit la methode de la derivee est plus eleguante

[xNiicO]

C'est vrai mais là ou je sèche est que pour la méthode de la dérivée je comprends pas, je sais que dans un temps j'utilisais le taux d'accroissement pour trouver les une limites lorsque h tend vers 0.

D'ailleurs tu me dis que le premier coefficient est
Or f(-1) n'est pas possible, sinon le dénominateur de f(x) s'annule et il y a une divison par 0 ce qui n'est pas possible, c'est pour ça que je ne comprends pas.

En revanche je voulais savoir si on pouvait faire :

Mais le problème du -1 persiste.

[mrif]

Quel est le but de faire ça ?

Pourquoi faire que le numérateur à chaque fois pour les nombres dérivées ?
Parce que le numérateur (dans ce cas) s'annule pour la veleur qui annule le dénominateur.

Donc ta première limite est f'(-1) et ta deuxième limite est g'(0).
f'(x) = 100x^99 + 2 et f'(-1) = -98
g'(x) = (1+tan²(x))e^(tan(x)) et g'(0) = 1

Correctif
f'(x) = 1000 x^999 + 2 et f'(-1) = -998

[busard_des_roseaux]

D'ailleurs tu me dis que le premier coefficient est

avec

[xNiicO]

Donc ta première limite est f'(-1) et ta deuxième limite est g'(0).
f'(x) = 100x^99 + 2 et f'(-1) = -98
g'(x) = (1+tan²(x))e^(tan(x)) et g'(0) = 1

Tu fais une dérivée seulement pour le numérateur, pourquoi ? et tes résultats vont te servir à quoi finalement après ?

Car c'est limite de f(x) que l'on veut pas et pas une partie de f(x) que l'on a en plus dérivée et calculé sa limite

[xNiicO]

avec

Très bien, donc finalement on obtient
Car f(-1)=0

Ce qui est notre point de départ finalement. Pour ça que sur papier quand je l'ai fait j'avais l'impression de tourner en rond.

[mrif]

Tu fais une dérivée seulement pour le numérateur, pourquoi ? et tes résultats vont te servir à quoi finalement après ?

Car c'est limite de f(x) que l'on veut pas et pas une partie de f(x) que l'on a en plus dérivée et calculé sa limite

Tu n'as pas compris la notion du nombre dérivé.
Comme l'a indiqué busard_des_roseaux,

Or =
Donc

Il reste à calculer la dérivée f'(x) et puis f'(-1) et tu trouveras bien -998

Même raisonnement pour la 2 ème limite.

[xNiicO]

J'ai parfaitement compris le raisonnement c'est bon, il me manque juste une chose, c'est de m'expliquer pourquoi vous prenez comme f(x) ceci :

et pas

[mrif]

J'ai parfaitement compris le raisonnement c'est bon, il me manque juste une chose, c'est de m'expliquer pourquoi vous prenez comme f(x) ceci :

et pas

On cherche à écrire la limite en -1 de sous forme d'un nombre dérivée d'une fonction f en -1. Si cette fonction f existe, on aura:
. Comme le numérateur s'annule en -1, ce numérateur est le candidat idéal pour f.

[xNiicO]

Parfait merci.

J'ai deux questions encore, bien que j'ai compris la méthode, c'est parfait mais j'aimerai m'assurer que les valeurs que j'ai trouvé soient vrai.

Pour la 1) notre limite est lorsque que x tend vers -1. Mais qu'en est-il lorsque x tend vers et . Car quand j'entre les valeurs très proche de la valeurs -1 je trouve pas systématiquement -998 environ, bon c'est proche donc pour cette limite je pense que la question se pose pas mais pour la 2) lorsque x tend vers et je n'obtiens pas la valeurs de la limite que j'ai trouvé à savoir 1. Je trouve soit un infini soit 0, quand je testes pour et .

L'autre question est plus en annexe, je trouve que cette méthode peut pas mal servir pour les limites assez complexes qui tendent vers une valeurs finies, est-ce qu'il est conseillé de l'utiliser quand les méthodes de factorisations ne sont pas suffisantes ?

[mrif]

Parfait merci.

J'ai deux questions encore, bien que j'ai compris la méthode, c'est parfait mais j'aimerai m'assurer que les valeurs que j'ai trouvé soient vrai.

Pour la 1) notre limite est lorsque que x tend vers -1. Mais qu'en est-il lorsque x tend vers et . Car quand j'entre les valeurs très proche de la valeurs -1 je trouve pas systématiquement -998 environ, bon c'est proche donc pour cette limite je pense que la question se pose pas mais pour la 2) lorsque x tend vers et je n'obtiens pas la valeurs de la limite que j'ai trouvé à savoir 1. Je trouve soit un infini soit 0, quand je testes pour et .

L'autre question est plus en annexe, je trouve que cette méthode peut pas mal servir pour les limites assez complexes qui tendent vers une valeurs finies, est-ce qu'il est conseillé de l'utiliser quand les méthodes de factorisations ne sont pas suffisantes ?

Donne les valeurs voisines de -1 (pour la première limite) et de 0 (pour la 2ème) que tu as prises et les résultats que tu a obtenus pour qu'on puisse trouver une explication.

Cette méthode s'applique quand on cherche la limite d'une fonction de la forme [f(x)-f(a)]/(x-a) quand x tend vers a.
exemple: trouver lim[(cos(x) -1)/x] quand x tend vers 0.
Qu'est ce qui joue le role de a?
Peut-on ecrire le numérateur sous la forme f(x) - f(a)?

Réponse:
x = x -0 donc a = 0.
1 = cos(0) donc f(x) = cos(x)
Donc la limite recherchée est -sin(0) = 0.

[xNiicO]

Merci du petit cours

Alors :

Pour la 1) :

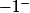
Pour j'ai fait un test avec -1.00001 et -1.00000000001 qui donne respectivement à la calculette environ -1003 et -998

Ce qui est vraie pour le moment

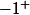
Pour j'ai fait un test avec -0.99999 et -0.99999999999 qui donne respectivement à la calculette environ -993 et -998

Ce qui est vraie donc pour la 1), j'ai du surement mal tapé tout à l'heure à la calculette pour le second.

Pour la 2) :

Pour j'ai testé avec 0.00001 et 0.00000000001 qui donne respectivement environ 0.0174 et 0

Ce qui pour le moment est faux car on a dit que c'était 1.

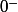
Pour j'ai testé avec -0.00001 et -0.00000000001 qui donne respectivement environ 0.0174 et 0

Ce qui donne aussi 0 et on a dit que c'était 1.

Je vais donc revoir mon calcul, correctement refaire ma dérivée car la calculette dit vraie donc pour moi si c'est 1 c'est que j'ai du bugué quelque part

[xNiicO]

Voici comment j'ai fait pour la 2)




J'ai fait votre raisonnement et j'ai aboutit sur la deuxième ligne, je ne marque pas le calcul intermédiaire.

Maintenant on note qui admet pour dérivée

Donc pour donc

Donc