Bonjour ,
en cours on a vu la définition formelle de limite "standard" et épointée d'une fonction , par standard je sous-entend que le point dont on cherche la limite est inclus.
je n'arrive pas saisir la différence fondamentale entre ces deux notions :mur: est ce que quelqu'un pourrait m'éclairer avec des exemples ou autre ?
Merci d'avance
Limites épointée
6 messages
- Page 1 sur 1
arnaud32 a écrit:peux tu nous donner tes deux definitions stp.
ce sont les même que celle-ci :
http://fr.wikipedia.org/wiki/Limite_(math%C3%A9matiques)#Limite_d.27une_fonction_en_un_point
A mon avis, les deux définitions, c'est :
- Limite "usuelle" :\Rightarrow...) qui donne la limite "usuelle"
qui donne la limite "usuelle" =L)
-Limite "épointé" : idem, mais avec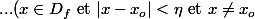\Rightarrow...) qui correspond à
qui correspond à 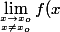=L)
Aprés, ben y'a des avantages et des inconvénients aux deux.
Par exemple, la fonction F nulle sur R sauf en 0 ou elle vaut 1 n'a pas de limite en 0 avec la première définition alors qu'avec la deuxième, elle tend vers 0 en 0.
Avec la première définition, pour traduire que f est continue en xo, il suffit de dire que la limite quand x tend vers xo existe (vu qu'avec cette définition, elle sera forcément égale à f(xo)). Par contre avec la deuxième définition, il faurt dire non seulement que la limite existe mais aussi qu'elle vaut f(xo).
Aprés, ce qui est embètant avec la deuxième définition, c'est que pour avoir le droit de calculer la limite en xo d'une fonction définie sur un domaine Df, ç'est plus compliqué qu'avec la première définition : dire que xo est dans l'adhérence de Df ne suffit plus (on ne peut pas calculer la limite "épointé" en un point isolé de Df...)
Aprés, si tu veut voir la différence entre les deux notions, ben y'a deux cas de figure :
- Soit n'est pas dans
n'est pas dans  et les deux définitions disent clairement la même chose.
et les deux définitions disent clairement la même chose.
- Soit est dans
est dans  et on a :
et on a : =L\ \Leftrightarrow\ \Big(\lim_{x\to x_o\atop x\not= x_o} f(x)=L\text{ et } f(x_o)=L\Big))
Pour donner mon opinion, je pense qu'en général et sans précision, c'est plutôt la deuxième définition qu'on utilise dans la pratique (celle qui dit que F tend vers 0 lorsque x tend vers 0 bien que F(0)=1) mais... on ommet souvent de le dire...
Et je rajouterais bien que, évidement, il faut comprendre que ce n'est pas la même chose, mais qu'il n'y a pas de quoi non plus en faire "tout un fromage"... :marteau:
- Limite "usuelle" :
-Limite "épointé" : idem, mais avec
Aprés, ben y'a des avantages et des inconvénients aux deux.
Par exemple, la fonction F nulle sur R sauf en 0 ou elle vaut 1 n'a pas de limite en 0 avec la première définition alors qu'avec la deuxième, elle tend vers 0 en 0.
Avec la première définition, pour traduire que f est continue en xo, il suffit de dire que la limite quand x tend vers xo existe (vu qu'avec cette définition, elle sera forcément égale à f(xo)). Par contre avec la deuxième définition, il faurt dire non seulement que la limite existe mais aussi qu'elle vaut f(xo).
Aprés, ce qui est embètant avec la deuxième définition, c'est que pour avoir le droit de calculer la limite en xo d'une fonction définie sur un domaine Df, ç'est plus compliqué qu'avec la première définition : dire que xo est dans l'adhérence de Df ne suffit plus (on ne peut pas calculer la limite "épointé" en un point isolé de Df...)
Aprés, si tu veut voir la différence entre les deux notions, ben y'a deux cas de figure :
- Soit
- Soit
Pour donner mon opinion, je pense qu'en général et sans précision, c'est plutôt la deuxième définition qu'on utilise dans la pratique (celle qui dit que F tend vers 0 lorsque x tend vers 0 bien que F(0)=1) mais... on ommet souvent de le dire...
Et je rajouterais bien que, évidement, il faut comprendre que ce n'est pas la même chose, mais qu'il n'y a pas de quoi non plus en faire "tout un fromage"... :marteau:
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
