Limite d’une suite
25 messages
- Page 1 sur 2 - 1, 2
Limite d’une suite
Bonjour, est ce qu’il y a une technique pour calculer la limite de la suite:
Sqrt( a1+sqrt (a2+sqrt(a3+….+sqrt(an)))…..) avec an une suite récurrente non constante ( car dans le cas où elle est constante, il suffit de consdérer la fonction f(x)= sqrt(a+x)
Merci d’avance.
Sqrt( a1+sqrt (a2+sqrt(a3+….+sqrt(an)))…..) avec an une suite récurrente non constante ( car dans le cas où elle est constante, il suffit de consdérer la fonction f(x)= sqrt(a+x)
Merci d’avance.
Re: Limite d’une suite
Salut,
Sans plus de précision concernant la formule de récurrence vérifiée par la suite_{n\geqslant1}) on ne peut pas dire grand chose, surtout concernant l'éventuelle limite (la convergence, par contre, c'est souvent relativement simple).
on ne peut pas dire grand chose, surtout concernant l'éventuelle limite (la convergence, par contre, c'est souvent relativement simple).
Sinon, un truc qu'on utilise assez fréquemment dans ce type de contexte, c'est d'écrire que ton (avec plein de racines), c'est un certain
(avec plein de racines), c'est un certain ) avec une formule de récurrence du type
avec une formule de récurrence du type =\sqrt{?+f_n(?)}) (où les ? ne sont pas les mêmes partout et dépende de la formule liant les
(où les ? ne sont pas les mêmes partout et dépende de la formule liant les  )
)
Sans plus de précision concernant la formule de récurrence vérifiée par la suite
Sinon, un truc qu'on utilise assez fréquemment dans ce type de contexte, c'est d'écrire que ton
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Limite d’une suite
Merci , ma suite (a_n ) vérifie la relation de récurrence suivante:
a_(n+1)= (a_(n)^2-12a_(n)+42)/6
Mais je n’arrive pas encore à trouver une relation algébrique qui me permet de calculer la limite.
a_(n+1)= (a_(n)^2-12a_(n)+42)/6
Mais je n’arrive pas encore à trouver une relation algébrique qui me permet de calculer la limite.
Re: Limite d’une suite
Dans ce cas, je pense qu'effectivement une bonne approche pourrait être d'écrire que ) où
où 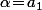 et où la suite de fonctions
et où la suite de fonctions _{n\geq 1}) est définie par
est définie par 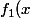\!=\!\sqrt{x}) puis
puis \!=\!\sqrt{x+f_n\big(\frac16(x^2\!-12x+42)\big)})
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Limite d’une suite
Ce qui me complique la chose c’est que d’un côté j’ai x et d’un autre (x^2-12x+42)/6 .
Puis-je avoir un autre coup de pouce ?
Merci.
Puis-je avoir un autre coup de pouce ?
Merci.
Re: Limite d’une suite
En fait, avec les valeurs numériques de ta suite récurrente, j'arrive pas à grand chose : en général, le premier truc qu'on fait, c'est de conjecturer la limite de la suite de fonction  sauf que là, j'arrive à rien . . .
sauf que là, j'arrive à rien . . .
Tu es absolument certaines de tes valeurs ?
Tu es absolument certaines de tes valeurs ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Limite d’une suite
Effectivement, je me suis trompée, c’est un 72 à la fin et non 42 .
Je m’excuse.
En calculant quelques termes de un, il semble que la limite est 6,5 . Comment le prouver?
Merci.
Je m’excuse.
En calculant quelques termes de un, il semble que la limite est 6,5 . Comment le prouver?
Merci.
Re: Limite d’une suite
Ben non, la limite n'est surement pas un simple réel mais une fonction vu que ça dépend évidement de la valeur initiale (inconnue) de la suite _{n\geq 1}) .
.
Par contre, avec 72 et pas 42, ce qu'on a, c'est que^2) ce qui permet d'avoir une formule close pour
ce qui permet d'avoir une formule close pour  en fonction de
en fonction de  et de l'inconnue
et de l'inconnue 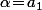 .
.
Par contre, avec 72 et pas 42, ce qu'on a, c'est que
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Limite d’une suite
La limite de fn est bien sûr une fonction, si mon calcul est bon, j’ai évoqué la limite de un en conjecturant que c’est 6,5.
Sinon pour an j’ai trouvé que an=6( 2^(2^n) +1) .
Mais comment ceci peut m’aider à trouver la fonction limite . Merci .
Sinon pour an j’ai trouvé que an=6( 2^(2^n) +1) .
Mais comment ceci peut m’aider à trouver la fonction limite . Merci .
Re: Limite d’une suite
Et ton  ça risque pas d'être ça non plus vu que ça dépend de l'inconnue
ça risque pas d'être ça non plus vu que ça dépend de l'inconnue 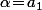 .
.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Limite d’une suite
Cherchant une fonction f telle que f(x)=racine( x+f( (x^2-12x+72)/6) sous forme de polynôme j’ai trouvé que f(x)= x/6 + 2
Mais …
Mais …
Re: Limite d’une suite
Effectivement, si  alors
alors  et on doit pouvoir montrer que
et on doit pouvoir montrer que  (et ce résultat perdure pour
(et ce résultat perdure pour 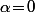 et
et  ).
).
Par contre, pour alors
alors  et c'est toujours mystère et boule de gomme concernant
et c'est toujours mystère et boule de gomme concernant ) : j'arrive uniquement à montrer que c'est convergent vers un
: j'arrive uniquement à montrer que c'est convergent vers un ) entre
entre  et
et  (voire plus précis) et je suis convaincu que c'est équivalent à du
(voire plus précis) et je suis convaincu que c'est équivalent à du  lorsque
lorsque  .
.
Par contre, pour
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Limite d’une suite
Dans l’énoncé que j’ai entre les mains a1=30 > 12 .
Donc je n’ai aucun espoir peut-être.
Donc je n’ai aucun espoir peut-être.
Re: Limite d’une suite
S’il vous plait est ce que je peux savoir comment vous avez obtenu cet encadrement ? Merci .
Re: Limite d’une suite
Pour un  fixé, la suite
fixé, la suite \big)_{n\geqslant1}) est croissante (vu qu'à chaque itération, on rajoute un truc positif à la fin de la cascade de racines carrées) et on montre facilement par récurrence sur
est croissante (vu qu'à chaque itération, on rajoute un truc positif à la fin de la cascade de racines carrées) et on montre facilement par récurrence sur  que, pour tout
que, pour tout  ,
, \leqslant\sqrt{\frac32x+5}) (on peut même faire légèrement mieux que 5).
(on peut même faire légèrement mieux que 5).
EDIT : sauf erreur, j'ai un peu mieux. Pour\!\geqslant\!\sqrt{\frac32 x-3})
EDIT : sauf erreur, j'ai un peu mieux. Pour
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Limite d’une suite
Pour x=30 , le calcul approchée que j’ai conjecturé, à savoir 6,5 vérifie bien : 6,5 >= racine(3/2 .30 -3) de manière très approchée.
Re: Limite d’une suite
Bonjour, je reste sur ma soif pour déterminer la valeur exacte .
Puis-je du moins comprendre l’idée de l’encadrement de fn(x) ?
Merci .
Puis-je du moins comprendre l’idée de l’encadrement de fn(x) ?
Merci .
25 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 86 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
