Limite d’une suite

[Sara1999]

Puis-je juste avoir un coup de pouce pour l’idée de démonstration? Merci.

[Ben314]

La grande difficulté (en tout cas pour moi), c'est de conjecturer la limite (qui doit vérifier la fameuse formule mais il y a des tas de fonctions qui vérifient ça).
Pour x entre 0 et 12 tu as trouvé toi même la formule. Pour x>12, je l'ai trouvé en faisant l'hypothèse qu'au voisinage de l'infini f(x) admet un développement asymptotique en et en cherchant (par identification) les coefficients.
Ensuite, pour prouver que la suite (fn) converge bien vers ce qu'on a conjecturé, il faut montrer que la fonction conjecturée est un majorant des fn (ce qui la plupart du temps est facile) et trouver un minorant variable (i.e. dépendant de n) de fn qui va tendre vers la fonction conjecturée. Et pour trouver un tel minorant, si par exemple la fonction conjecturée est de la forme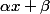 , tu regarde pour quels a,b,A,B l' implications f_n>ax+b => f_{n+1}>Ax+B est vrai (sur ton domaine d'étude) et tu avise en fonction de ce que tu trouve.

[Sara1999]

Merci infiniment, c’est magnifique comme preuve. Je l’ai lue et très bien assimilée . Je ne pouvais y arriver toute seule.

[Ben314]

En ce qui me concerne, ça m'a bien amusé et il me semble bien que je ne connaissait pas le résultat (mais bon, avec l'age, j'ai un peu l'Alzheimer, donc c'est pas très sûr . . .).
Donc merci pour ce joli problème.

[Sara1999]

Merci à vous Monsieur .
«  Il y a des êtres qui justifient le monde , qui aident à vivre par leur seule présence » .
Je remplace dans cette citation d’Albert Camus , le mot “ Êtres ” par “ problèmes de math ” .