Limite d'une suite
30 messages
- Page 1 sur 2 - 1, 2
Bonjour, par une étude de fonction tu peux montrer assez facilement que l'équation que tu donnes a deux solutions, l'une étant 0 et l'autre étant comprise entre 1 et 2. La deuxième solution ne peut s'exprimer à partir des fonctions de base (il faut recourir au W de Lambert) mais on peut l'approcher par des méthodes numériques (elle vaut environ 1,26).
Skullkid a écrit:Bonjour, par une étude de fonction tu peux montrer assez facilement que l'équation que tu donnes a deux solutions, l'une étant 0 et l'autre étant comprise entre 1 et 2. La deuxième solution ne peut s'exprimer à partir des fonctions de base (il faut recourir au W de Lambert) mais on peut l'approcher par des méthodes numériques (elle vaut environ 1,26).
En répondant à Marcopolo20 de cette manière, tu ne l'aides pas à bien écrire l'énoncé de ses exercices. Il a parlé de suite mais pas d'équations (Toujours des devinettes)
J'ai trouver merci. Il est vrai que j'ai écrire une équation mais c'était pour ne pas avoir à écrire la suite qui me paraissait évidente au vu de l'équation mais je comprend maintenant que cela n'est pas rigoureux.
Ensuite, il faut montrer que pour tout entier n, Un est dans l'intervalle [1;alfa]
et Uo=1 ; L=alfa donc cela me paraît logique que Un soit situé entre son minimum et sa limite mais je ne vois pas comment le montrer.
Merci de votre aide
Ensuite, il faut montrer que pour tout entier n, Un est dans l'intervalle [1;alfa]
et Uo=1 ; L=alfa donc cela me paraît logique que Un soit situé entre son minimum et sa limite mais je ne vois pas comment le montrer.
Merci de votre aide
deltab a écrit:détailles un peu pour voir
on a Uo=1 et
où pour tout x>-1/2, g(x)=ln(1+2x)
J'ai montrer que :
- g(alfa)=alfa avec la partie précédente de l'exo.
- que pour tout x appartenant à [1;alfa], 0<=g'(x)<=(2/3)
- que la suite Un est strictement positive
Comme on a L=ln(1+2L)=g(L) j'en déduis que L=alfa
[quote="deltab"]Passes par l'étude de la fonction ) , tu pourras peut-être conclure.
, tu pourras peut-être conclure.
J'ai étudier la fonction g mais je n'y arrive pas.
Il faut aussi montrer que Un est strictement monotone mais pour ça, il faut montrer que Un>Un-1 et je ne vois pas comment, est-ce que le fait que g soit croissante est suffisant.
J'ai étudier la fonction g mais je n'y arrive pas.
Il faut aussi montrer que Un est strictement monotone mais pour ça, il faut montrer que Un>Un-1 et je ne vois pas comment, est-ce que le fait que g soit croissante est suffisant.
Bonjour
1) Si g est continue monotone, quelle alors l'image g(I) d'un intervalle I=[a,b].
2) Que peux-tu dire sur la suite) (monotonie) si tu connais le signe de h(x)=x-f(x)
(monotonie) si tu connais le signe de h(x)=x-f(x)
3) L'existence de la solution >0 de l'équation
de l'équation ) a été affirmé par Skullkid (sans entrer dans les détails de la démonstration), peux-tu le démontrer?
a été affirmé par Skullkid (sans entrer dans les détails de la démonstration), peux-tu le démontrer?
PS: fais moi savoir quand tu seras en ligne. Moi, je reviens dans une heure.
marcopolo20 a écrit:deltab a écrit:Passes par l'étude de la fonction, tu pourras peut-être conclure.
J'ai étudier la fonction g mais je n'y arrive pas.
Il faut aussi montrer que Un est strictement monotone mais pour ça, il faut montrer que Un>Un-1 et je ne vois pas comment, est-ce que le fait que g soit croissante est suffisant.
1) Si g est continue monotone, quelle alors l'image g(I) d'un intervalle I=[a,b].
2) Que peux-tu dire sur la suite
3) L'existence de la solution >0
PS: fais moi savoir quand tu seras en ligne. Moi, je reviens dans une heure.
deltab a écrit:Bonjourmarcopolo20 a écrit:1) Si g est continue monotone, quelle alors l'image g(I) d'un intervalle I=[a,b].
2) Que peux-tu dire sur la suite(monotonie) si tu connais le signe de h(x)=x-f(x)
3) L'existence de la solution >0de l'équation
a été affirmé par Skullkid (sans entrer dans les détails de la démonstration), peux-tu le démontrer?
PS: fais moi savoir quand tu seras en ligne. Moi, je reviens dans une heure.
1)il y a une bijection : g est continue et strictement croissante sur ]-1/2;+infini[ à valeurs dans [1;alfa] donc g réalise une bijection de ]-1/2;+infini[ dans [1;alfa], en particulier, on a donc : pour tout réel x appartenant à [1;alfa], 1>=g(x)>=alfa mais comme Un tend vers alfa 1>=g(Un)<=alfa non ?
2) je ne vois pas a quoi correspond h(x)=x-f(x) mais pour connaître les variations de la suite
j'étudies le signe de Un+1-Un
3) Dans la partie précédente de mon exo, j'ai montré que f(alfa)=0 ie : (ln(1+2x)/x)-1=0
soit g(alfa)/alfa=1 donc g(alfa)=alfa
Bonjour.
Je vais supposer, en attendant l'énoncé qu'on demande de montrer que la suite) définie par
définie par  =1 et
=1 et ) est convergente. Pour cela, on va montrer qu'elle monotone bornée.
est convergente. Pour cela, on va montrer qu'elle monotone bornée.
1) Bornée.
L'étude de la fonction=\ln(1+2x)) montre qu'elle positive croissante sur
montre qu'elle positive croissante sur  .
.
Si on peut trouver un intervalle borné tel que G(I) subset I , les éléments de la suite vont donc appartenir à I et la suite sera bien bornée. On a
borné tel que G(I) subset I , les éléments de la suite vont donc appartenir à I et la suite sera bien bornée. On a =0) . Si on peut trouver un point
. Si on peut trouver un point 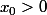 tel que
tel que =x_0) on aura
on aura  et même
et même  . Considérons la fonction h(x)=x-g(x) , elle est continue et vérifie
. Considérons la fonction h(x)=x-g(x) , elle est continue et vérifie =1-\ln(3)=\ln(e)-\ln(3) 0) , le TVI appliqué à
, le TVI appliqué à  et la croissance de h (sur [1,2] assure l'existence d'une solution unique de l'équation h(x)=0. En notant par
et la croissance de h (sur [1,2] assure l'existence d'une solution unique de l'équation h(x)=0. En notant par  cette solution, on aura
cette solution, on aura  d'où le résultat: la suite
d'où le résultat: la suite ) est bornée.
est bornée.
2) Monotonie.
Son étude sera faite en étudiant le signe de h(x)=x-g(x) sur l'intervalle [0,\alpha].
A demain après-midi
Je vais supposer, en attendant l'énoncé qu'on demande de montrer que la suite
1) Bornée.
L'étude de la fonction
Si on peut trouver un intervalle
2) Monotonie.
Son étude sera faite en étudiant le signe de h(x)=x-g(x) sur l'intervalle [0,\alpha].
A demain après-midi
Bonjour.
Même si on arrive au même résultat concernant la convergence de la suite (U_n), la démarche que je proposais de faire et celle de l'énoncé sont différentes. Je garde les notations de l'énoncé de l'exercice.
1) Remarque hors sujet: L'étude de la fonction aurait été plus simple si on avait pris
aurait été plus simple si on avait pris =x^2(1+2x)f'(x)) au lieu de
au lieu de =x^2f'(x)) .
.
2) a été déterminé grâce au TVI appliqué à f.
a été déterminé grâce au TVI appliqué à f.
3) Tu as été bloqué au niveau de l'équation=\ln(1+2L)) (Partie 2) question 4). On a déjà 2 solutions
(Partie 2) question 4). On a déjà 2 solutions 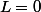 à exclure et
à exclure et  , la réponse à la question 1) devrait donner :
, la réponse à la question 1) devrait donner : =\alpha) . (Reste à montrer que \alpha est unique)
. (Reste à montrer que \alpha est unique)
4) Question 5-a) Il suffit de montrer que \subset [1,\alpha]) .
.
5) Question 5-b) Étudies le signe de la fonction=g(x)-x) sur
sur  . Que peut-on conclure sur le signe de
. Que peut-on conclure sur le signe de 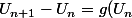-U_n) ?
?
marcopolo20 a écrit:Bonjour,
Voici les liens
https://mega.co.nz/#!PMJ3VIqC!MLcYGXCMv ... -EOrRQ8OxY
https://mega.co.nz/#!6AxGjQqY!HsyqKU1rg ... gE42dFpx4I
Même si on arrive au même résultat concernant la convergence de la suite (U_n), la démarche que je proposais de faire et celle de l'énoncé sont différentes. Je garde les notations de l'énoncé de l'exercice.
1) Remarque hors sujet: L'étude de la fonction
2)
3) Tu as été bloqué au niveau de l'équation
4) Question 5-a) Il suffit de montrer que
5) Question 5-b) Étudies le signe de la fonction
30 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
