Limite d'une suite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
MacErmite
- Membre Relatif
- Messages: 408
- Enregistré le: 12 Mai 2006, 12:00
-
 par MacErmite » 13 Mar 2010, 14:06
par MacErmite » 13 Mar 2010, 14:06
Bonjour,
J'ai une suite de nombres complexes telle que
=0)
et je cherche à connaître

Alors j'ai écris ceci :
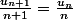
Soit :
} - \frac{(n+1).u_n}{n.(n+1)} = 0)
après simplification :
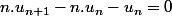
ce qui conduit à :

Donc :
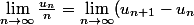=0)
??
Ce raisonement est il correct ??
Merci.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 13 Mar 2010, 14:14
par Nightmare » 13 Mar 2010, 14:14
Salut !
Euh, pourquoi

?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 13 Mar 2010, 14:15
par Nightmare » 13 Mar 2010, 14:15
Connais-tu le lemme de Cesaro?
-
MacErmite
- Membre Relatif
- Messages: 408
- Enregistré le: 12 Mai 2006, 12:00
-
 par MacErmite » 13 Mar 2010, 14:18
par MacErmite » 13 Mar 2010, 14:18
non je ne connais pas.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 13 Mar 2010, 14:40
par Nightmare » 13 Mar 2010, 14:40
Notons
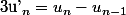
Tu remarques que
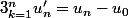
Il s'agit donc de calculer

Pour cela, tu sais que

tend vers 0 donc qu'à partir d'un certain rang N, elle est majorée par un certain

. Essaye donc de couper ta somme en deux (les termes avant N et après N) et de regarder ce qu'il se passe.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 13 Mar 2010, 14:46
par barbu23 » 13 Mar 2010, 14:46
Le leme de Cesaro stipule que si une suite

converge vers

, alors sa moyenne arithmetique converge aussi vers

.
On trouve cette même notion dans d'autres branches de mathematiques , par exemple, en theorie des probabilités et plus exactement le theorème de la limite centrale, ou bien en theorie des distributions, ou il s'avère impossible de considerer l'image d'un point par une distribution ( qui est une idée propre pour les fonctions et applications ), et on la remplace par sa moyenne arithmetique continue ( c'est à dire l'integrale ) ! :happy3:
 par alavacommejetepousse » 13 Mar 2010, 18:26
par alavacommejetepousse » 13 Mar 2010, 18:26
barbu23 a écrit:Le leme de Cesaro stipule que si une suite

converge vers

, alors sa moyenne arithmetique converge aussi vers

.
On trouve cette même notion dans d'autres branches de mathematiques , par exemple, en theorie des probabilités et plus exactement le theorème de la limite centrale, ou bien en theorie des distributions, ou il s'avère impossible de considerer l'image d'un point par une distribution ( qui est une idée propre pour les fonctions et applications ), et on la remplace par sa moyenne arithmetique continue ( c'est à dire l'integrale ) ! :happy3:
hum le théorème central limite parle bien d une limite d une moyenne arithmétique des Xi mais ( Xn) ne converge pas seule la moyenne converge.
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 13 Mar 2010, 19:26
par Sylviel » 13 Mar 2010, 19:26
hum le théorème central limite parle bien d une limite d une moyenne arithmétique des Xi mais ( Xn) ne converge pas seule la moyenne converge.
Plop : la moyenne arithmétique converge bien en loi... La convergence de l'espérance c'est la loi (forte) des grands nombres.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
 par alavacommejetepousse » 13 Mar 2010, 23:09
par alavacommejetepousse » 13 Mar 2010, 23:09
Sylviel a écrit:Plop : la moyenne arithmétique converge bien en loi... La convergence de l'espérance c'est la loi (forte) des grands nombres.
je ne sais pas ce que signifie plop mais je n'ai jamais parlé d'espérance
la loi forte des grands nombres assûre qu'il y a convergence VERS l'espérance avec probabilité 1
la loi faible : convergence vers l'espérance en probabilité
-
MacErmite
- Membre Relatif
- Messages: 408
- Enregistré le: 12 Mai 2006, 12:00
-
 par MacErmite » 27 Mar 2010, 17:23
par MacErmite » 27 Mar 2010, 17:23
Nightmare a écrit:Notons
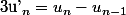
Tu remarques que
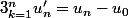
Il s'agit donc de calculer

Pour cela, tu sais que

tend vers 0 donc qu'à partir d'un certain rang N, elle est majorée par un certain

. Essaye donc de couper ta somme en deux (les termes avant N et après N) et de regarder ce qu'il se passe.
En posant
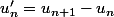
; alors
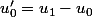
;
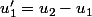
;
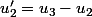
;
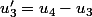
alors
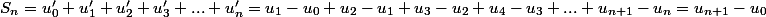
J'ai essayé de retrouver la forme que tu me conseilles , mais c'est pas gagné ...
 par taib_le_mathemagicien » 28 Mar 2010, 14:51
par taib_le_mathemagicien » 28 Mar 2010, 14:51
c on pourrait utiliser la suite de cesaro ce sera tres pratique et ca nous donne la limite tres facilement
posons vn =u(n+1)-u(n) qui tend vers 0 selon la definition donc
(v(0)+....v(n))\n ------>lim(vn)=0 or cette expression est egale a (u(n)-u(0))\n
et le tour est joué :zen:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
converge vers
, alors sa moyenne arithmetique converge aussi vers
.
tend vers 0 donc qu'à partir d'un certain rang N, elle est majorée par un certain
. Essaye donc de couper ta somme en deux (les termes avant N et après N) et de regarder ce qu'il se passe.