Limite d'une racine de polynôme
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mathelot
 par mathelot » 15 Fév 2007, 15:08
par mathelot » 15 Fév 2007, 15:08
bonjour,
un défi , ça vous tente ?
soit
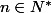
1) Quel est le nombre de racines du polynome
=x^{n}-2x+1)
dans l'intervalle ]0;1[
2) soit
)
une suite de réels de ]0;1[ tels que
=0)
La suite (

) converge t elle ?
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 15 Fév 2007, 16:47
par tize » 15 Fév 2007, 16:47
Bonjour,
pour la 1) je dirai que le polynôme

admet n racines distinctes autrement dit qu'il ne possède pas de racines doubles car sinon une telle racine (double) serait aussi racine du polynôme dérivé dont on connait toutes les racines :
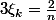^{\frac{1}{n-1}}e^{i\frac{k2\pi}{n-1}})
(k compris entre 0 et n-2) et qui ne peuvent pas (après calculs...) être racines de notre polynôme...
[EDIT] : sauf pour n=2
-
Tcheby
- Messages: 9
- Enregistré le: 15 Fév 2007, 14:31
-
 par Tcheby » 15 Fév 2007, 17:01
par Tcheby » 15 Fév 2007, 17:01
ta solution ne marche déjà pas pour n=2
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 15 Fév 2007, 17:07
par tize » 15 Fév 2007, 17:07
Tcheby a écrit:ta solution ne marche déjà pas pour n=2
J'ai vu, j'ai modifié mon dernier post mais sinon ça marche !
Attends je refais les calculs et les envoies
-
Tcheby
- Messages: 9
- Enregistré le: 15 Fév 2007, 14:31
-
 par Tcheby » 15 Fév 2007, 17:12
par Tcheby » 15 Fév 2007, 17:12
je suis pas sur de bien comprendre la question 2, la suite n'est pas bien définie puisque le polynôme admet plusieurs racines
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 15 Fév 2007, 17:18
par tize » 15 Fév 2007, 17:18
=nx^{n-1}-2=n\(x^{n-1}-\frac{2}{n}\))
les racines sont donc :
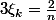^{\frac{1}{n-1}}e^{i\frac{k2\pi}{n-1}}\quad(0\leq k<n-1))
Si

était une racine de

alors
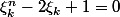
ce qui revient à (avec
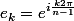
) :
^{\frac{n}{n-1}}e_k-2e_k+1=0)
donc :
^{\frac{n}{n-1}}\)=1)
donc
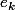
est réel et vaut 1 et
^{\frac{n}{n-1}}=1)
donc n=2
Pour la question 2, la réponse doit être indépendante du choix des racines...
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 15 Fév 2007, 17:34
par fahr451 » 15 Fév 2007, 17:34
pour n impair Pn a trois racines réelles
1 une autre positive et une négative
donc en prenant x(2p) = 1 et x(2p+1) = la racine négative la suite x ne converge pas.
-
mathelot
 par mathelot » 15 Fév 2007, 19:26
par mathelot » 15 Fév 2007, 19:26
je suis vraiment confus: il y a une erreur dans l'énoncé:
il fallait lire nombre de racines dans ]0;1[ !!! je corrige.
on s'intéresse qu'aux racines dans ]0;1[.
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 16 Fév 2007, 12:20
par tize » 16 Fév 2007, 12:20
Bonjour,
après cette correction, je reviens sur ce problème :
Supposons qu'il existe deux racines réelles
<0)
, donc d'après le TVI

admet une et une seule racine dans ]0;1[
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités