Limite d'une intégrale

[H2H2]

Pouvez vous m'aider à trouver :

Soit f continue de [0,1] dans R. Soit n élément de N.

limite quand n tend vers + infini de l'intégrale entre 0 et 1 de n*f(t)*exp(-n*t) dt ?

[Mikou]

je pense que la limite est 0

[Tqup3]

Essaye 2 IPP, tu devrais aperçevoir une chose intéréssante :++:

Moi je pense que la limite est f(0), corrigez moi si j'ai tort.

[H2H2]

Oui, la limite est f(0), désolé, j'avais oublié de le dire.
Merci, je vais essayer les IPP... Sinon je pensais faire |l'integrale - f(0)| et majorer mais j'ai pas trouvé... :cry:

[daiski]

indication :
utilises le résultat général suivant après l'avoir établi :
si g est une fonction continue sur I = [a b] et f une fonction C1 positivie décroissante sur I alors il existe c entre a et b tel que :
int(a->b) [f(t)g(t)dt] = f(a)*int(a->c)[g(t)dt]

dans notre cas g c'est f et f c'est t -> n*exp(-nt)

ça donne lim = lim quand n -> infini de f(0) (1 - exp(-cn)) dans notre cas d'où le résultat .

le résultat ci haut n'est as difficile à prouver : utilises une primitive de f dans g s'annulant en a et une intégration par parties en exploitant le fait que la primitive d'une fct continue est continue donc bornée sur un int fermé borné etc.puis le tVI..(c'est un peu long mais faisable et plus instructif= c'est le cas général ) :we:

[H2H2]

J'ai essayé mais je trouve pas, mon intégrale empire... ou en tout cas j'arrive pas à voir ce qu'il faudrait voir...
Tu es sur qu'il faut intégrer par parties sachant que f est continue mais pas C1 ? On ne peut qu'intégrer f et dériver n*exp(-n*t) non ?

Ca me donne (en appelant F une primitive de f et G une primitive de F) :

n*F(1)*exp(-n)-n*F(0)+n^2*exp(-n)*G(1)-n^2*G(0)+int(n^3*exp(-n*t) dt)

Et si à la deuxieme intégration je dérive F pour redonner f, je tombe sur 0=0.

Ou est ce que je me trompe ? :help:

[abcd22]

Bonjour !
En effet, ça marche en faisant intégrale - f(0) : on a , donc , donc .
Soit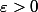 , comme f est continue en 0, on peut choisir a tel que . On coupe l'intégrale en , on majore le premier morceau par en utilisant l'hypothèse sur a.
Pour le 2e, , ça tend vers 0 quand n tend vers l'infini, et tend aussi vers 0. On a donc une majoration par 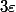pour n assez grand.

[daiski]

H2h2:
la méthode marche n'essaie pas de la démontrer , d'abord appliques et assures toi que ça marche pour la démonstration c'est pas dur du tout crois moi , .. y'a pas de confusion , on aura besoin de t->exp(-nt) C1 ce qui est vérifié et de f continue pour pouvoir parler d'un primitive d'elle , je ne c pas d'où ça sort la primitive de la primitive de f dans ton raisonnement , une simple intégration par parties. peut être j'ai mal expliqué , je prendrai le temps de l'écrire en détail si t'y arrive tjrs pas .

[H2H2]

Merci abcd22, peut etre un peu difficile a trouver comme ca mais bon, ca marche...

Merci daiski, je vais essayer, j'avais repondu quand tu répondais en même temps... j'essaye et je te dis.

[abcd22]

En fait c'est un raisonnement assez classique de séparer une intégrale en plusieurs morceaux pour les majorer séparément, la raison pour laquelle je fais ça ici c'est que quand n tend vers l'infini, fait un pic en 0 et est presque nulle ailleurs, ce qui fait que quand n tend vers l'infini, il n'y a que les valeurs de f proches de 0 qui ont une influence sur l'intégrale, c'est comme ça qu'on trouve la valeur de la limite :
pour n assez grand, pour x > a et (car 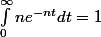, mais toute la fonction est concentrée en 0),
f est continue en 0 donc il existe a > 0 tel que pour x < a, ,
donc pour n assez grand, .
Evidemment ce que je viens de faire n'est pas du tout rigoureux, mais la démonstration que j'ai donnée est juste la formalisation de ce raisonnement. Si tu n'as jamais vu de démonstrations de ce style ce n'est pas évident, ça vient avec l'habitude.

[H2H2]

Désolé daiski mais je bloque... Je vois pas comment faire l'integ par partie. Qu'est ce qu'on derive, qu'est ce qu'on integre ? Est ce qu'on en fait deux ?
T'es pas obligé de tout bien ecrire si ca te prend trop de temps mais si tu me dis les principales etapes, je devrais m'en sortir.

merci

[Tqup3]

Pour l'IPP:
u=f(t)
u'=f'(t)

v'=ne^(-nt)
v=-e^(-nt)

Tu refais la même pour la deuxieme et tu verras apparaître une relation de récurrence.

[H2H2]

J'ai aussi une autre question :we: ... :

J'arrive pas à calculer : int(0->Pi/2,sin((2n+1)t)/sin(t) dt).
Je sais pas comment trouver un lien entre dérivée et primitive à cause de ce 2n+1 ... pour utiliser les regles de Bioche par ex...

[H2H2]

Mais f n'est pas forcement dérivable sur I. On peut pas utiliser f'(t) si ?

[daiski]

pour cette dernière intégrale , si on la note In pour tout n € IN elle existe car la fonction dedans est prolongeable par continuité en 0.
et pour tout entier In+1 - In = 0 (formules trigo) donc In est constante et vaut I0 (i zéro) à caculer séparément. résulat = pi/2

[daiski]

Pour l'IPP:
u=f(t)
u'=f'(t)

v'=ne^(-nt)
v=-e^(-nt)

Tu refais la même pour la deuxieme et tu verras apparaître une relation de récurrence.

non
rien ne nous dit que f est dérivable , par contre elle est primitivable :zen:

[Tqup3]

Arf, autant pour moi :mur:

[H2H2]

daiski, qu'est ce que je fais avec int(F(t)*n^2*exp(-nt) dt) ?

[H2H2]

Merci pour l'autre intégrale au fait.
Si tu peux tout m'expliquer pour la première ca serait sympa (sans ecrire tous les calculs bien sur).
Merci

[daiski]

dsl j'avais quitté le poste.
ben voilà pour la première intégrale dans le cas général dont j'ai donné l'énonçé plus loin :

je reprend les notations : g fontion continue sur I = [a b]
f C1 surI positive et décroissante sur I.
question : montrons qu'il exite c dans [a b] tel que int(a->b)[f(t)g(t)dt = f(a) * int(a->c)[g(t)dt]

l'idée est de montrer que la valeur suivante : int(a->b)[f(t)g(t)dt / f(a) est prise par la fonction G définie par G = int(a->x)[g(t)dt) (donc la primitive de g qui s'annule en a , qui existe et est C1 puisque g est continue)

on peut écrire en utilisant une intégration par parties :

int(a->b)[f(t)g(t)dt] = f(b)*G(b) - int(a->b)[f'(t)G(t)dt]

G étant continue sur le segment [a b] elle y est bonée et atteint ses bornes .notons les m et M.

on a : pour tout t € I m =< G(t) =< M et f'(t) =< 0

donc : pour tout t € I Mf'(t) =< f'(t)G(t) =< mf'(t)

et en intégrant entre a et b :

M(f(b) - f(a)) =< int(a->b)[f'(t)G(t)]dt =< m(f(b) - f(a))

puis mf(a) =< f(b)G(b) + m(f(a) - f(b)) =< int(a->b)[f(t)g(t)]dt =< M(f(a) - f(b)) + f(b) G(b) =< Mf(a) (c'est juste du calcul qu'il faut faire soigneusement )

ainsi si f(a) #0 alors

on aura établi que m =< int(a->b)[f(t)g(t)dt / f(a) =< M

TVI ==> existence de C (car G(I) = [m M])

sinon si f(a) = 0 alors puisque f est décroissante positive , elle est identiquement nulle sur I et là tout c entre a et b vérifiera l'égalité demandée.

voilà , j'espèreque c'est clair , c'est juste l'idée du TVI et de la primitive qui peut séduire , le calcul est nul :we: