Limite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 08 Sep 2019, 20:08
par mehdi-128 » 08 Sep 2019, 20:08
Bonsoir,
On a
 \leq f(x) \leq \lim_b f)
(1)
Supposons qu'il existe
=\lim_b f)
Je ne comprends pas comment obtenir la suite

Alors pour tout
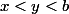
on aurait :
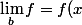 < f(y) \leq \lim_b f)
ce qui est impossible.
En fait l'inégalité
 \leq \lim_b f)
provient de (1) mais je ne comprends pas d'où sort le
)

-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 08 Sep 2019, 20:15
par mehdi-128 » 08 Sep 2019, 20:15
Non en fait c'est une question stupide, j'ai trouvé la solution !
f est strictement croissante donc f(x) < f(y) et la contradiction provient du fait que lim_b f < lim_b f
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités

