Limite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
C.l
- Membre Relatif
- Messages: 109
- Enregistré le: 11 Juin 2013, 19:48
-
 par C.l » 05 Jan 2014, 19:49
par C.l » 05 Jan 2014, 19:49
Bonsoir,
j'ai du mal à calculer cette limite et je ne comprend pas le corrigé,
voici la limite: f(x)= x+1/ (1/x) sinx
Merci pour votre aide!!
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 05 Jan 2014, 19:59
par Manny06 » 05 Jan 2014, 19:59
C.l a écrit:Bonsoir,
j'ai du mal à calculer cette limite et je ne comprend pas le corrigé,
voici la limite: f(x)= x+1/ (1/x) sinx
Merci pour votre aide!!
Manque-t-il des parenthèses ?
En quel point cherches-tu la limite ?
-
C.l
- Membre Relatif
- Messages: 109
- Enregistré le: 11 Juin 2013, 19:48
-
 par C.l » 05 Jan 2014, 20:19
par C.l » 05 Jan 2014, 20:19
Manny06 a écrit:Manque-t-il des parenthèses ?
En quel point cherches-tu la limite ?
Ah oui pardon en + infini!
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 06 Jan 2014, 12:02
par deltab » 06 Jan 2014, 12:02
Bonjour.
Si
=x +\dfrac{\sin x}{x})
, je ne vois pas de difficulté pour le calcul de la limite de
)
quand
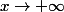
.
Si
=x +\dfrac{1}{x\sin x})
, c'est autre chose.
-
C.l
- Membre Relatif
- Messages: 109
- Enregistré le: 11 Juin 2013, 19:48
-
 par C.l » 06 Jan 2014, 13:33
par C.l » 06 Jan 2014, 13:33
deltab a écrit:Bonjour.
Si
=x +\dfrac{\sin x}{x})
, je ne vois pas de difficulté pour le calcul de la limite de
)
quand
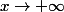
.
Si
=x +\dfrac{1}{x\sin x})
, c'est autre chose.
c'est (x+1) / ((1/x)sinx)
il manquait des parenthèses désolée :-/
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 06 Jan 2014, 13:36
par Manny06 » 06 Jan 2014, 13:36
C.l a écrit:c'est (x+1) / ((1/x)sinx)
il manquait des parenthèses désolée :-/
cela semble difficile car x²+x tend vers +infini et sinx change de signe
-
C.l
- Membre Relatif
- Messages: 109
- Enregistré le: 11 Juin 2013, 19:48
-
 par C.l » 06 Jan 2014, 21:27
par C.l » 06 Jan 2014, 21:27
Manny06 a écrit:cela semble difficile car x²+x tend vers +infini et sinx change de signe
Mais il y a une méthode?
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 07 Jan 2014, 04:19
par deltab » 07 Jan 2014, 04:19
Bonjour.
C.l a écrit:Mais il y a une méthode?
La fonction à considérer est donc
=\dfrac{x+1}{\dfrac{\sin x}{x}}=\dfrac{x(x+1)}{\sin x})
à moins que maintenant il y a des parenthèses en plus .
Pour parler de limite en

, il faut déjà que la fonction soit définie dans un intervalle
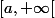
, est-ce que c'est le cas pour
=\dfrac{x+1}{\dfrac{\sin x}{x}}=\dfrac{x(x+1)}{\sin x})
ou
=x+\dfrac{1}{x\sin x})
ou encore
=\dfrac{x+1}{x\sin x})
?
-
C.l
- Membre Relatif
- Messages: 109
- Enregistré le: 11 Juin 2013, 19:48
-
 par C.l » 07 Jan 2014, 23:29
par C.l » 07 Jan 2014, 23:29
deltab a écrit:Bonjour.
La fonction à considérer est donc
=\dfrac{x+1}{\dfrac{\sin x}{x}}=\dfrac{x(x+1)}{\sin x})
à moins que maintenant il y a des parenthèses en plus .
Pour parler de limite en

, il faut déjà que la fonction soit définie dans un intervalle
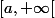
, est-ce que c'est le cas pour
=\dfrac{x+1}{\dfrac{\sin x}{x}}=\dfrac{x(x+1)}{\sin x})
ou
=x+\dfrac{1}{x\sin x})
ou encore
=\dfrac{x+1}{x\sin x})
?
Non elle n'est pas défini, enfin l'énnoncé c'était juste calculer la limite.
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 08 Jan 2014, 00:36
par deltab » 08 Jan 2014, 00:36
Bonsoir.
Calculer une limite ne veut pas dire que la limite existe.
Autre exemple: limite de
)
quand
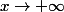
-
bneay
- Membre Naturel
- Messages: 53
- Enregistré le: 06 Jan 2014, 23:04
-
 par bneay » 08 Jan 2014, 01:48
par bneay » 08 Jan 2014, 01:48
Avec la règle de l'hôpital c'est facile, toutes les conditions sont vérifiées, enfin la limite, s'elle existe, est finie.
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 10 Jan 2014, 14:12
par deltab » 10 Jan 2014, 14:12
Bonjour.
bneay a écrit:Avec la règle de l'hôpital c'est facile, toutes les conditions sont vérifiées, enfin la limite, s'elle existe, est finie.
Tu as pris quelle fonction? et attention au sinus, il s'annule une infinité de fois sur tout intervalle
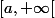
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
à moins que maintenant il y a des parenthèses en plus .
, il faut déjà que la fonction soit définie dans un intervalle
, est-ce que c'est le cas pour
ou
ou encore
?
