Limite suite cosh
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
savan-306D
- Membre Naturel
- Messages: 64
- Enregistré le: 24 Nov 2013, 23:39
-
 par savan-306D » 25 Avr 2014, 21:13
par savan-306D » 25 Avr 2014, 21:13
Salut,
j'ai une suite
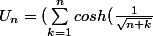) -n)
je dois calculer la limite
ce que j'ai essayé, c'est d'utiliser les suites de reimann mais sans résultat

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 25 Avr 2014, 23:46
par Ben314 » 25 Avr 2014, 23:46
Salut,
Tu es sûr de ton énoncé ?
Parce que là, la limite, elle est triviale vu que cosh(x) est équivalent en +oo à exp(x)/2 donc rien que le premier terme cosh(racine(n+1)) l'emporte largement sur le malheureux -n (voire même sur 'les' -n s'il font partie de la somme)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
savan-306D
- Membre Naturel
- Messages: 64
- Enregistré le: 24 Nov 2013, 23:39
-
 par savan-306D » 26 Avr 2014, 13:24
par savan-306D » 26 Avr 2014, 13:24
Non, j'ai fait une erreur dans l'énoncé, sinon ça serait évident.
c'est 1/racine(n+k) non pas racine(n+k) je vais modifier
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 26 Avr 2014, 15:01
par Maxmau » 26 Avr 2014, 15:01
savan-306D a écrit:Salut,
j'ai une suite
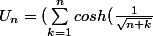) -n)
je dois calculer la limite
ce que j'ai essayé, c'est d'utiliser les suites de reimann mais sans résultat
Bj
essaie d'utiliser un développement de Taylor Lagrange de Chx entre 0 et x à l'ordre 4.
avec x = 1/rac(k+n)
le terme "1" va te permettre de simplifier avec n (quand tu fais la somme)
je pense que le terme en x² va te donner une somme de Riemann......
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités