Limite de référence
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par legeniedesalpages » 26 Déc 2007, 02:34
par legeniedesalpages » 26 Déc 2007, 02:34
Bonsoir,
je ne vois pas comment montrer que
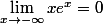
?
Merci pour vos indications.

-
Argentoratum
- Membre Relatif
- Messages: 231
- Enregistré le: 12 Sep 2007, 22:35
-
 par Argentoratum » 26 Déc 2007, 08:40
par Argentoratum » 26 Déc 2007, 08:40
Je ne sais plus comment le démontrer mais ce que je peux te dire, c'est de garder en tête le fait que l'exponentielle "l'emporte" sur x (et sur les polynômes en général). Voilà désolé de ne pas pouvoir t'aider, bonne chance.
 par legeniedesalpages » 26 Déc 2007, 10:02
par legeniedesalpages » 26 Déc 2007, 10:02
Argentoratum a écrit:Je ne sais plus comment le démontrer mais ce que je peux te dire, c'est de garder en tête le fait que l'exponentielle "l'emporte" sur x (et sur les polynômes en général). Voilà désolé de ne pas pouvoir t'aider, bonne chance.
Oui je me souviens de cette phrase, je ne savais pas que ça marchait aussi quand

.
En fait cette limite résiste sec, je vais regarder si je peux pas trafiquer avec le log.

-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 26 Déc 2007, 10:23
par yos » 26 Déc 2007, 10:23
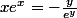
avec y=-x.
 par legeniedesalpages » 26 Déc 2007, 10:48
par legeniedesalpages » 26 Déc 2007, 10:48
yos a écrit: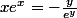
avec y=-x.
Bonjour yos,
donc tu me conseilles de passer à une forme indéterminée du type
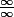
, c'est plus facile à lever?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 26 Déc 2007, 11:01
par Nightmare » 26 Déc 2007, 11:01
Salut :happy3:
On pose x=ln(y)
On cherche donc la limite quand y tend vers 0+ de ln(y)y.
Soit en posant t=1/y la limite quand t tend vers +oo de -ln(t)/t
Or :
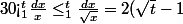<2\sqrt{t})
ie:
}{t}<\frac{2}{\sqrt{t}}\longrightarrow_{t\to +\infty} 0)
CQFD
:happy3:
 par legeniedesalpages » 26 Déc 2007, 11:07
par legeniedesalpages » 26 Déc 2007, 11:07
ok merci jord, je regarde ça tout de suite.
Pour en revenir à la méthode de yos, je suis allé regardé sur cette page:
[url=http://fr.wikipedia.org/wiki/Indétermination_de_la_forme_;)/;)]http://fr.wikipedia.org/wiki/Indétermination_de_la_forme_;)/;)[/url]
j'ai l'impression qu'il y a un souci:
comment on peut dire du fait que

que

?
 par legeniedesalpages » 26 Déc 2007, 11:11
par legeniedesalpages » 26 Déc 2007, 11:11
Nightmare a écrit:Salut :happy3:
On pose x=ln(y)
On cherche donc la limite quand y tend vers 0+ de ln(y)y.
Soit en posant t=1/y la limite quand t tend vers +oo de -ln(t)/t
Or :
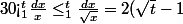<2\sqrt{t})
ie:
}{t}<\frac{2}{\sqrt{t}}\longrightarrow_{t\to +\infty} 0)
CQFD
:happy3:
ok explication très claire, merci jord

-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 26 Déc 2007, 11:44
par yos » 26 Déc 2007, 11:44
legeniedesalpages a écrit:donc tu me conseilles de passer à une forme indéterminée du type
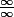
, c'est plus facile à lever?
Je pensais que tu supposais connu la limite de exp(x)/x en

. Si c'est pas le cas, tu peux là prouver avec

(évident en étudiant

) qui donne

puis

.
 par legeniedesalpages » 26 Déc 2007, 12:39
par legeniedesalpages » 26 Déc 2007, 12:39
yos a écrit:Je pensais que tu supposais connu la limite de exp(x)/x en

. Si c'est pas le cas, tu peux là prouver avec

(évident en étudiant

) qui donne

puis

.
ah oui effectivement, quel couillon je suis :marteau:
merci yos

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 13 invités