Limite: problème en l'infini
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
aze321
- Membre Naturel
- Messages: 49
- Enregistré le: 15 Fév 2008, 19:27
-
 par aze321 » 11 Mar 2008, 21:52
par aze321 » 11 Mar 2008, 21:52
Bonjour,
comment démontrer que

tends vers 0?
avec

l'écart moyen et

la moyenne des x_i?
cordialement,
jp

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 11 Mar 2008, 22:00
par nuage » 11 Mar 2008, 22:00
Salut,
je ne suis pas sûr de bien comprendre.
Mais si

et

ne dépendent pas de

il n'y a pas vraiment de problème :
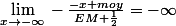
du moins si, comme c'est extrémement vraisemblable

-
Magemax
- Messages: 4
- Enregistré le: 11 Mar 2008, 18:30
-
 par Magemax » 11 Mar 2008, 22:03
par Magemax » 11 Mar 2008, 22:03
Grâce au Théoreme Centrale limite (et au Théorème de Slutsky), tu sais que
racine(n)*(x-moy)/EM converge vers une loi normale centrée réduite de parametres 0 et 1.
si x est la moyenne empirique de n variables iid ayant une variance, moy la vraie espérance d'une de ces variables la et EM l'ecart type réel (ou empirique) de la même série
Donc (x-moy)/EM converge presque surement vers 0 quand n tend vers l'infini.
Ensuite, tu utilises le fait que f:x->-(exp(x)/2)/2+1/2 est continue, et pour les puristes un théorème de continuité pour les variables aléatoires.
donc f[ (x-moy)/EM ] converge presque surement vers f(0) = 0
-
aze321
- Membre Naturel
- Messages: 49
- Enregistré le: 15 Fév 2008, 19:27
-
 par aze321 » 11 Mar 2008, 22:30
par aze321 » 11 Mar 2008, 22:30
Bonjour nuage! (merci pour ton aide comme d'hab')
Non en fait la moyenne
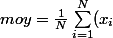)
et l'écart moyen
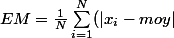)
varient bien en fonction des

qui dépendent tous d'une même loi et je dois démontrer que lorsque l'un de ces

tend vers

alors
)
tends vers

.
cordialement,
jp
-
aze321
- Membre Naturel
- Messages: 49
- Enregistré le: 15 Fév 2008, 19:27
-
 par aze321 » 11 Mar 2008, 22:36
par aze321 » 11 Mar 2008, 22:36
Bonjour Magemax,
Merci aussi pour ton aide mais je dois bien avoué que je n'ai pas compris, peut-être aussi que je n'étais pas trop clair, peux-tu revenir un peu plus en détail par rapport à ma précédente réponse?
jp

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 12 Mar 2008, 00:15
par nuage » 12 Mar 2008, 00:15
Je crois que je n'avais pas bien compris ton problème.
D'une certaine façon il me reste obscur : je ne vois pas comment un nombre aléatoire peut tendre vers quoi que ce soit avec une loi constante.
Sinon en fixant tous les

sauf un

qui tend vers

je trouve

ce qui n'est pas très satisfaisant pour démontrer ton résultat.
En attendant des précisions,
A+
nuage :
Ps : Ce qui précède est à

fixe. L'idée de
Magemax est sans doute meilleure mais on a alors a trouver la limite quand
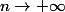
-
aze321
- Membre Naturel
- Messages: 49
- Enregistré le: 15 Fév 2008, 19:27
-
 par aze321 » 12 Mar 2008, 10:34
par aze321 » 12 Mar 2008, 10:34
Bonjour nuage (décidement tu ne dors jamais

)
En fait, on n'aucune information sur

le nombre d'observation.
Sinon, peux-tu m'expiquer comment tu obtiens ce résultat

?
merci,
JP
ps: il y a un bug avec les balises latex lorsque tu veux afficher

il faut mettre un espaces avant et après le signe moins sinon ça affiche cela


-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 13 Mar 2008, 23:17
par nuage » 13 Mar 2008, 23:17
Salut,
avec mes excuses, j'ai fait une erreur grossière en oubliant un facteur 2.
Disons que

et que les

pour

sont constants avec
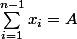
.
On a
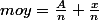
pour

assez proche de

on a
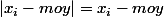
donc :
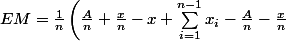= \frac1{n}\left(\frac{A}{n} +\frac{x}{n}-x + A -\frac{n-1}{n} A - \frac{n-1}{n} x\right)= -2 x\frac{n-1}{n^2}+\frac{ 2 A}{n^2})
On en tire : au voisinage de


Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités