Limite par epsilon et delta!
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Saraaa
- Messages: 4
- Enregistré le: 22 Sep 2018, 16:41
-
 par Saraaa » 22 Sep 2018, 16:47
par Saraaa » 22 Sep 2018, 16:47
Bonjour ou bonsoir!
J'ai besoin d'aide

Question:
"montrer que si f admet une limite finie en x0 alors il existe n>0 tel que f soit bornée sur ]x0-n,n+x0[ "
Comment prouver l'existence de n ? ça fait toute une après-midi que j'essaie de comprendre

!
-
Saraaa
- Messages: 4
- Enregistré le: 22 Sep 2018, 16:41
-
 par Saraaa » 22 Sep 2018, 16:52
par Saraaa » 22 Sep 2018, 16:52
J'ai la correction de la question mais je ne vois pas comment en prenant epsilon=1 prouve son existence
Modifié en dernier par
Saraaa le 22 Sep 2018, 16:54, modifié 1 fois.
-
LB2
- Habitué(e)
- Messages: 1504
- Enregistré le: 05 Nov 2017, 16:32
-
 par LB2 » 22 Sep 2018, 16:53
par LB2 » 22 Sep 2018, 16:53
Bonjour,
Essaie d'appliquer la définition de "f admet une limite finie en x0" avec epsilon = 1, par exemple
-
Saraaa
- Messages: 4
- Enregistré le: 22 Sep 2018, 16:41
-
 par Saraaa » 22 Sep 2018, 16:58
par Saraaa » 22 Sep 2018, 16:58
Je ne comprends pas pourquoi

Je ne comprends pas pourquoi ce raisonnement là
-
LB2
- Habitué(e)
- Messages: 1504
- Enregistré le: 05 Nov 2017, 16:32
-
 par LB2 » 22 Sep 2018, 18:50
par LB2 » 22 Sep 2018, 18:50
Je pense qu'il faut que tu travailles davantage la logique, les propositions, les quantificateurs, la négation pour pouvoir comprendre le raisonnement.
Est-ce que tu peux écrire avec les quantificateurs la définition de la proposition "f admet une limite finie l en x0" ?
-
Saraaa
- Messages: 4
- Enregistré le: 22 Sep 2018, 16:41
-
 par Saraaa » 23 Sep 2018, 00:22
par Saraaa » 23 Sep 2018, 00:22
Je suis en début d'une année prépa donc ce genre de raisonnement mathématique est assez nouveau pour moi ^^ je comprends les notations ( il existe , quelque sois,.. ) mais ça reste quand même assez floue

je ne comprends pas comment ce raisonnement a pu le résoudre
P
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 23 Sep 2018, 02:18
par infernaleur » 23 Sep 2018, 02:18
Salut,
Comme f admet une limite finie en

alors on a :
=l)
où l est un réel ce qui ce traduit :

tel que
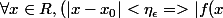-l|<\epsilon))
Comme cette "phrase" est vrai pour tout

strictement positif tu peux par exemple prendre
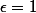
(tu peux tout aussi prendre 2 ou bien 5 ou bien

si ça te fait plaisir le plus important est juste de prendre un nombre
strictement positif )
Tu as donc :

tel que
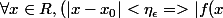-l|<1))
Après à toi de savoir manipuler des valeurs absolues le résultat en découle.
-
LB2
- Habitué(e)
- Messages: 1504
- Enregistré le: 05 Nov 2017, 16:32
-
 par LB2 » 23 Sep 2018, 13:01
par LB2 » 23 Sep 2018, 13:01
Saraaa a écrit:Je suis en début d'une année prépa donc ce genre de raisonnement mathématique est assez nouveau pour moi ^^ je comprends les notations ( il existe , quelque sois,.. ) mais ça reste quand même assez floue

je ne comprends pas comment ce raisonnement a pu le résoudre
P
c'est normal mais il faut que tu comprennes la définition de la limite "avec les epsilon", et que tu saches l'écrire avec les bons quantificateurs, pour pouvoir traduire le français en langage mathématique et réciproquement.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 17 invités


 Je ne comprends pas pourquoi ce raisonnement là
Je ne comprends pas pourquoi ce raisonnement là je ne comprends pas comment ce raisonnement a pu le résoudre
je ne comprends pas comment ce raisonnement a pu le résoudre je ne comprends pas comment ce raisonnement a pu le résoudre