Merci d'avence.
Limite infinie
6 messages
- Page 1 sur 1
Limite infinie
Bonsoir peut être que la réponse a ma question est évidente mais je n'arrive pas a comprendre ce résultat :
^{\frac{1}{n}}) =
= 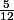
Merci d'avence.
Merci d'avence.
Re: Limite infinie
je t'ai proposé deux étapes .
Tu ne me parles que de la première .
Dans la deuxième , 1/n n'est plus un exposant .
La limite de la parenthèse est élémentaire(suites géo dont le module de la raison est inférieur à 1 , domination d'une fonction carré par une suite géométrique ,...)
Tu ne me parles que de la première .
Dans la deuxième , 1/n n'est plus un exposant .
La limite de la parenthèse est élémentaire(suites géo dont le module de la raison est inférieur à 1 , domination d'une fonction carré par une suite géométrique ,...)
Re: Limite infinie
tournesol a écrit:Il suffit de mettre en facteur les termes dominants :
ton expression est égale à
je comprends toujours pas le passage
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
