Limite difficile

[Dufhead]

Bonjour ,

Est-ce que quelqu'un arriverai à trouver la limite de x.e^(-3/x) en 0 ?
Il s'agit d'étudier la continuité de la fonction en 0.
Normalement il faudrait trouver 0 car f(0)=0. Mais je ne sais pas comment m'y prendre.

Merci

[vincentroumezy]

En 0+ ou 0- ?
En 0+, c'est trivial, puisque -3/x tend vers -l'infini, donc l'exponentielle tend vers 0 et x aussi.

[manoa]

Salut!

en 0- tu peux poser t=-1/x par exemple :)

[alm]

Salut

une aute idée est de calculer :

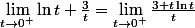
[Dufhead]

Salut merci pour vos réponses

J'ai trouvé en 0+ car x.e^(-3/x) = x/e^(3/x)
Par contre en 0- je vois pas trop meme en posant t=-1/x quel est le principe? Je trouve 0.+oo
Et 0*0 est une forme indéterminée

[alm]

Salut

Vous avez certainement vu dans votre cours des limites standards à connaitre comme
non?

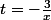
je prefére d'ailleur que tu poses , comme ça tu as

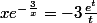
Remarque:
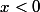
comme pour on a on a alors :
et là de nouveau ton cours donne
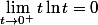
Il en résulte que:
[CENTER] [/CENTER] et c'est à toi de terminer.

[Dufhead]

Merci bien pour tes conseils, j'ai compris!

Meilleurs voeux pour la nouvelle année!

[alm]

Je t'en prie Dufhead
Merci et à toi aussi mes meilleurs voeux pour la nouvelle année.

[Dufhead]

Par contre je ne comprends pas, avec la premiere méthode je trouve -oo , avec la deuxieme je trouve 0 !

[Dufhead]

Ne serait-ce pas plutot: ln(-f(x)) = ln(-x) -3/x = (xln(-x) -3) / x = (-xln(-x) +3) / -x ?
Donc lim de ln(-f(x)) en 0- = +oo et lim de f(x) = -oo ?

[alm]

Salut,

Ne serait-ce pas plutot: ln(-f(x)) = ln(-x) -3/x = (xln(-x) -3) / x = (-xln(-x) +3) / -x ?
Donc lim de ln(-f(x)) en 0- = +oo et lim de f(x) = -oo ?

Tout à fait Dufhead ! il me manque un sigane moins derière la fraction ...

Je vois que tu a bien lu l'indication . Bravo !

[Dufhead]

Salut,




Tout à fait Dufhead ! il me manque un sigane moins derière la fraction ...

Je vois que tu a bien lu l'indication . Bravo !

Merci de la réponse, je l'attendais pour etre sur

Bonne soirée