Lim

[fastandmaths]

Bonjour ,

je cherche à déterminer la

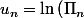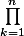
Ma première intuition c 'est de poser la suite pour me débarrasser du sauf que avec les sommes rien ne me saute au yeux même en cherchant respectivement un minorant et un majorant.

[GaBuZoMeu]

Somme de Riemann ?

[fastandmaths]

Justement je m’interrogeais sur ce point.

Pour moi et sauf erreur majorer par n' est pas suffisant pour passer à la limite .Idéalement il faudrait aussi le minorant et c 'est là que réside toute la difficulté ?

[fastandmaths]

j 'avais effectivement pensé à ce qui se passait à droite de , la somme de Riemann convergerait vers mais bon j ai abandonné l'idée

Qu'en pensez vous?

[GaBuZoMeu]

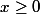
Tu ne connais pas de minorant de pour qui ferait le travail ici ?

[fastandmaths]

non je ne connais de minorant , en revanche je sais que pour positif et c 'est ce que j'ai utilisé pour trouver le majorant

[GaBuZoMeu]

Dommage. Tu ne connais pas non plus le d.l. de à l'origine ? Ça pourrait te guider pour trouver un minorant.

[fastandmaths]

Je ne connais rien pour le moment sur le développement limité , raisons pour laquelle j 'ai peut être fais l'impasse .Pour le majorant , c 'est plutôt classique et se démontre de plusieurs façons ( accroissement ..signe etc)

[fastandmaths]

je viens de trouver ceci sur le web dl de

donc l'inégalité c'est

Du coup, je m'arrête à quel degré ?

[GaBuZoMeu]

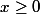
Bon, parlons accroissements. On peut effectivement démontrer la majoration pour par le fait que les deux fonctions s'annulent en et qu'on a l'inégalité sur les dérivées . Une fonction sympa qui ferait un joli minorant de ?

Le dl te souffle la réponse.

[fastandmaths]

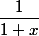
Oui si on parle des accroissements les fonctions s 'annulent en 0 . Le Dl me souffle la réponse c 'est à dire ? je dois trouver un minorant en regardant le Dl ?

[GaBuZoMeu]

N'oublie pas qu'on compare les dérivées. La "dérivée du dl" te souffle un minorant de la dérivée, oui.

[fastandmaths]

Oui je vois le truc le dl de est obtenu par intégration du développement de 1/(1+x)

[GaBuZoMeu]

Alors, cette minoration ?

[fastandmaths]

je m' arrette à

[fastandmaths]

x-(x^2/2)

[GaBuZoMeu]

Et ensuite ?

[fastandmaths]

Désolé , je n 'ai pas pu répondre plus tôt.J'ai pris le temps de me documenter sur les approximations polynomiale
Pour répondre à la question,
Ensuite je n 'ai plus qu'a considérer cette inégalité .On y voit que des sommes de Riemann.

En réalité, on en déduit que converge vers

ainsi,

[GaBuZoMeu]

Si tu veux ne voir que des sommes de Riemann, ça serait plutôt



À part ça, OK.