Lieux Géométrique

[damdamdoumdu36]

Alors voilà je vous met en pièce jointe la figure géométrique. Il faut que je démontre quelle forme géométrique les points J et I construisent lorsque je fais varier M sur le segment [AB]

Je vois clairement que le point J d'écrit un quart de cercle dont le centre est le milieu du segment [AD] mais pourquoi ? Et pour I je n'ai aucune idée.

Merci de m'éclairer de vos lumières :lol3:


PS: Je ne sais pas comment on met une piece jointe donc je vous donne une photo de la figure.

Lien

[chan79]

Salut
Pas facile de répondre; il faut mettre le texte de la construction.
Si AJD est rectangle en J, son cercle circonscrit a comme diamètre [AD] et il passe par J.
Pour I, tu peux conjecturer avec geogebra par exemple

[damdamdoumdu36]

Salut
Pas facile de répondre; il faut mettre le texte de la construction.
Si AJD est rectangle en J, son cercle circonscrit a comme diamètre [AD] et il passe par J.
Pour I, tu peux conjecturer avec geogebra par exemple

Alors pour le protocole c'est simple, on prend un carré de 1 cm de côté. On place M un point sur le segment [AB], ensuite on trace la droite (DM).
On prend la perpendiculaire à la droite (DM) passant par A. Elle coupe (DM) en J et [BC] en N. Suite on prend le segment [NM] et on met I milieu de [NM].

[chan79]

Alors pour le protocole c'est simple, on prend un carré de 1 cm de côté. On place M un point sur le segment [AB], ensuite on trace la droite (DM).
On prend la perpendiculaire à la droite (DM) passant par A. Elle coupe (DM) en J et [BC] en N. Suite on prend le segment [NM] et on met I milieu de [NM].

C'est bien ce que je pensais.
Le segment qui relie les milieux de [BC] et [BA] semble passer par I, quelle que soit la position de M sur [AB].

[damdamdoumdu36]

C'est bien ce que je pensais.
Le segment qui relie les milieux de [BC] et [BA] semble passer par I, quelle que soit la position de M sur [AB].

Ah ok Donc I décrit le segement reliant les milieux des segments [AB] et [BC].
Mais je ne vois pas comment l'expliquer mathématiques.
Idem pour le J Pourquoi est ce qu'il s'arrête au 1/4 du cercle.

En tout cas merci de tes réponses.

[chan79]

Idem pour le J Pourquoi est ce qu'il s'arrête au 1/4 du cercle.

.

M ne se déplace que sur [AB].
Sinon, tu pourrais placer un repère mais il y a sans doute mieux.

AMD et ABN sont isométriques
AM=BN

[damdamdoumdu36]

M ne se déplace que sur [AB].
Sinon, tu pourrais placer un repère mais il y a sans doute mieux.
On dirait que AM=BN

exact, AM=BN

[chan79]

exact, AM=BN

Projette M et I sur (BC) parallèlement à (AC).

[damdamdoumdu36]

Projette M et I sur (BC) parallèlement à (AC).

Salut excuse moi pour la réponse tardive, alors je viens de projeter M et I sur [BC] parallèlement à [AC]. Il coupe respectivement [BC] en E et F.

[damdamdoumdu36]

On a remarque que E est fixe et que N et F sont symétrique par rapport à E.

Lien2

[damdamdoumdu36]

Du coup je viens de remarquer que J et M sont symétrique par rapport à la bissectrice formée par les droites (AN) et (MF).

[chan79]

Les trois segments rouges ont la même longueur
Dans le triangle MNF, comme I est le milieu de [MN] et comme (IE) et (MF) sont parallèles, E est le milieu de [NF].
AM=BN et AM=CF donc BN=CF et E est le milieu de [BC].
Tu montres de même que (IE) coupe (AB) en son milieu.

C'est quand même plus simple avec un repère comme

[damdamdoumdu36]

Ok je viens de comprendre, juste petite chose comment sais tu que AM=BN ?

[chan79]

Ok je viens de comprendre, juste petite chose comment sais tu que AM=BN ?

et sont égaux (complémentaires avec le même angle)
Ecris qu'ils ont la même tangente.

[damdamdoumdu36]

Ok donc si j'ai bien compris pour I:

ADM et BAF sont des triangles égaux (car les angles sont tous les memes). Donc AM=BN.
De plus I milieu de MN et (IE) // (FM) donc E milieu de [BC].
De même I milieu de MN et (IG) // (NH) donc G milieu de [AB]
Donc I décrit le segment [EG] où E et G sont les milieux respectifs de [BC] et [AB].

[damdamdoumdu36]

Alors en faites je viens de me rendre compte que dans l'énoncé il veulent que j'exprime I e fonction de x où x coordonnée de M dans (A,B,D).

Voici le lien de l'énoncé:

Lien3

[damdamdoumdu36]

petit up car il y a un souci.

[damdamdoumdu36]

petit up car il y a un souci.

Bon alors je viens de trouver que I(x)=x-0,5 pour tout x compris entre 0,5 et 1. Mais je ne vois absolument pas comment je peux le justifier (pourquoi c'est cette réponse là).
Avez-vous une idée ?

[damdamdoumdu36]

Bon finalement j'ai réussi à prouver que I((x+1)/2,x/2).
Donc finalement I est la moitié se retrouve à la moitié tout le temps donc I décrit le segment EG où E et G milieu de [BC] et [AB]

Maintenant reste à bien justifier 2b) et à faire le 1)

[Robic]

Partons de I((x+1)/2,x/2) (j'ai refait les calculs, c'est bien ça).

On a donc :
;
.

(Ce que j'ai noté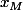 , c'est le x de l'énoncé. Je préfère garder x pour l'abscisse courante dans le repère.)

Du coup ça donne une relation du type , où je te laisse trouver a et b, qui prouve que I appartient à la droite d'équation y=ax+b (ici x est l'abscisse courante, pas le x de l'énoncé). Comme de plus 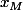parcourt un certain intervalle, le point I parcourt un certain segment. Pour déterminer ce segment, on détermine le point I lorsque 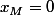puis le point I lorsque 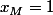, ce sont en effet E et G.