Les suites .....!!!!!

par **mostdu95** » 09 Déc 2007, 21:47

BONSOIR
ça une demi heure que je beug comletement sur cet exo...

est une a termes >0 Mq si

tend vers l alors

je n'ai aucune idee ...........debloquez moi s'il vous plait
et merci d'avance

par **Antho07** » 09 Déc 2007, 21:49

manque la question.
je suppose que la question c'est :

montrer que (Un)^(1/n) tend vers l

par **fati** » 09 Déc 2007, 22:10

j'ai po compris l'exo est ce que tu peux bien l'écrire!!

par **mostdu95** » 09 Déc 2007, 22:16

nn c'est l'implication qu'il faut montrer (merci d'abord pr vos reponses)

montrer que si

tend vers l alors

tend aussi vers l

par **mostdu95** » 09 Déc 2007, 22:28

nn c'est l'implication qu'il faut montrer (merci d'abord pr vos reponses)

montrer que si

tend vers l alors

tend aussi vers l

par **isortoq** » 10 Déc 2007, 08:04

mostdu95 a écrit:nn c'est l'implication qu'il faut montrer (merci d'abord pr vos reponses)

montrer que si tend vers l alors tend aussi vers l

Bonjour !

Si tu connais le th. de Cesaro, c'est quasi-immediat. En posant :

d'où

et donc, par Cesaro, on a :

et c'est facile de finir...

Sans Cesaro, il faut écrire :

pour

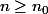
, et donc

puis elever ça à la puissance

... et continuer un peu...