Les sous-groupes de (Z,+)

par **protozik10012** » 23 Sep 2018, 11:13

Bonjour

Pouvez-vous m'expliquer pourquoi les sous groupes de Z sont les nZ?

Merci pour votre aide!

par **hdci** » 23 Sep 2018, 11:49

Bonjour,

Il y a deux aspects à voir : montrer que l'ensemble

est un groupe (facile), puis montrer que si

est un groupe alors il est de la forme

.

Pour cela :

donc

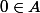
(comme c'est un groupe il contient l'élément neutre)

Si

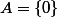
alors on a

.

Sinon, il existe

tel que

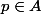
. Puisque

est un groupe,

. Donc

possède au moins un entier strictement positif (en l'occurrence,

)
Posons

le plus petit de ces entiers strictement positifs appartenant à

.

Il ne vous reste plus qu'à montrer qu'alors

: l'inclusion

est facile, et pour l'inclusion inverse, il suffit de raisonner par l'absurde.