Les résolutions des equations différentielles
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
lyrah
- Membre Naturel
- Messages: 47
- Enregistré le: 15 Avr 2006, 10:00
-
 par lyrah » 19 Avr 2006, 11:07
par lyrah » 19 Avr 2006, 11:07
Merci beaucoup :we:
En fiat j'ai fiat la même chose avec une autre equation mais je bloque sur un système car il a une forme particulière mais ej ne sais pas l'utilisé! je bloque ne fiat au second étapes
l'equation est celle là: y' - y = ( x² -1 ) exp(-x) et y(0) =0
donc en 1ère étape j'ai trouvé y = k exp(x)
Et j'ai fait exactement ce que vous m'avez montré et je j'arrive à
A'(x) = ( x² - 1 ) exp(-2x) mais ça c'est trop long à resoudre il n'y a pas un moyen plus facile?
-
Touriste
- Membre Relatif
- Messages: 278
- Enregistré le: 14 Avr 2006, 14:45
-
 par Touriste » 19 Avr 2006, 11:56
par Touriste » 19 Avr 2006, 11:56
Avec deux IPP, tu trouves une primitive de A'. Ce n'est pas si long que ça !
-
lyrah
- Membre Naturel
- Messages: 47
- Enregistré le: 15 Avr 2006, 10:00
-
 par lyrah » 19 Avr 2006, 12:03
par lyrah » 19 Avr 2006, 12:03
c'est quoi IPP?
-
Zeitblom
- Membre Naturel
- Messages: 90
- Enregistré le: 12 Juil 2005, 12:48
-
 par Zeitblom » 19 Avr 2006, 12:11
par Zeitblom » 19 Avr 2006, 12:11
IPP, c'est intégration par parties. Ici, c'est le x^2-1 qui t'embête : tu vas donc intégrer l'exponentielle et dériver ce morceau là. Alternativement, tu peux chercher une primitive sous la forme d'un polynôme multiplié par exp(-2x), dériver et identifier les coefficients.
-
lyrah
- Membre Naturel
- Messages: 47
- Enregistré le: 15 Avr 2006, 10:00
-
 par lyrah » 19 Avr 2006, 13:30
par lyrah » 19 Avr 2006, 13:30
:hum: don tout d'abord j'intègre
exp(-2x) c'est bien ça? donc ce qui me donnera
-exp(-2x)/2 et ensuite je dois dériver quoi exactement? je n'ai aps très bien compris :mur:
-
Touriste
- Membre Relatif
- Messages: 278
- Enregistré le: 14 Avr 2006, 14:45
-
 par Touriste » 19 Avr 2006, 14:14
par Touriste » 19 Avr 2006, 14:14
Pour te rafraîchir les idées (du moins je l'espère !)
v(x)dx = [u(x)v(x)]_a^b - \int_a^b u(x)v'(x)dx)
.
D'autre part,
dt)
est une primitive de A'.
-
lyrah
- Membre Naturel
- Messages: 47
- Enregistré le: 15 Avr 2006, 10:00
-
 par lyrah » 19 Avr 2006, 14:50
par lyrah » 19 Avr 2006, 14:50
:hum: donc si je prend la formule le u(x) ici c'est (x² -1) et v(x) = exp(-x)
c'est ça? et puis je fais l'intégrale?
-
Touriste
- Membre Relatif
- Messages: 278
- Enregistré le: 14 Avr 2006, 14:45
-
 par Touriste » 19 Avr 2006, 14:51
par Touriste » 19 Avr 2006, 14:51
Oui c'est ça. Ca ne te dis rien les intégrations par parties ? Peux-tu me dire quelle terminale tu as fait et ce que tu fais maintenant stp ?
-
lyrah
- Membre Naturel
- Messages: 47
- Enregistré le: 15 Avr 2006, 10:00
-
 par lyrah » 19 Avr 2006, 18:29
par lyrah » 19 Avr 2006, 18:29
Non ça me dit rien du tout l'integrale par partie, je viens du terminale STIE et je suis en DUT génie électrique. Et peux tu m'expliquer comment ça fonctionne cette methode et plus clairement possible si c'est possible merci
-
lyrah
- Membre Naturel
- Messages: 47
- Enregistré le: 15 Avr 2006, 10:00
-
 par lyrah » 20 Avr 2006, 12:10
par lyrah » 20 Avr 2006, 12:10
Est ce qu'on peut utiliser une autre manière de faire l'étape2?
-
Touriste
- Membre Relatif
- Messages: 278
- Enregistré le: 14 Avr 2006, 14:45
-
 par Touriste » 20 Avr 2006, 15:41
par Touriste » 20 Avr 2006, 15:41
Voici le détail pour l'IPP (je ne connais pas d'autre méthode pour ce calcul, mais tu vas voir ce n'est pas diabolique). On veut calculer
 = \int_0^x (t^2-1)exp{-2t} dt)
.
On va faire une IPP. On pose :
=exp{-2t})
=>
=-\frac{1}{2}exp{-2t})
=t^2-1)
=>
=2t)
D'après la formule d'IPP, on a donc
=\left[ -\frac{1}{2}exp{-2t}(t^2-1) \right]_1^x - \int_1^x -\frac{1}{2}exp{-2t}2tdt)
,
ce qui se réécrit
=-\frac{1}{2}exp{-2x}(x^2-1) + \int_1^x exp{-2t}tdt)
.
Pour calculer l'intégrale restante, on va à nouveau faire une IPP. On pose :
=exp{-2t})
=>
=-\frac{1}{2}exp{-2t})
=t)
=>
=1)
D'après la formule d'IPP, on a donc
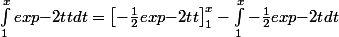
,
ce qui se réécrit
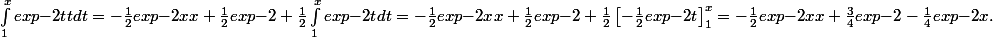
Donc, finalement,
=-\frac{1}{2}exp{-2x}x^2 -\frac{3}{2}exp{-2x}x + \frac{3}{4}exp{-2})
.
-
lyrah
- Membre Naturel
- Messages: 47
- Enregistré le: 15 Avr 2006, 10:00
-
 par lyrah » 30 Avr 2006, 20:13
par lyrah » 30 Avr 2006, 20:13
le resultat finale c'est bien
y = exp(x) * ( (1/3) x^3)
est c exact?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
 = \int_0^x (t^2-1)exp{-2t} dt) .
.=exp{-2t}) =>
=> =-\frac{1}{2}exp{-2t})
=t^2-1) =>
=> =2t)
=\left[ -\frac{1}{2}exp{-2t}(t^2-1) \right]_1^x - \int_1^x -\frac{1}{2}exp{-2t}2tdt) ,
,=-\frac{1}{2}exp{-2x}(x^2-1) + \int_1^x exp{-2t}tdt) .
.=exp{-2t}) =>
=> =-\frac{1}{2}exp{-2t})
=t) =>
=> =1)
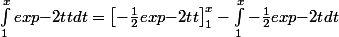 ,
,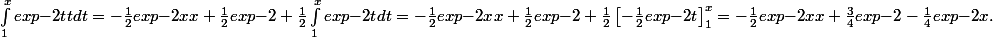
=-\frac{1}{2}exp{-2x}x^2 -\frac{3}{2}exp{-2x}x + \frac{3}{4}exp{-2}) .
.