Simpi a écrit:ensuite

car
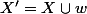
qui appartient à
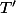
Je crois que cela ne suffit pas:
Tu as
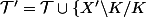
est un compact de

Pour démontrer q'une partie

de
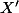
est un élément de

, tu dois prouver que

ou qu'il existe un compact

de

tel que
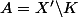
.
Tu fait ça pour
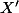
si tu veux bien démontrer que

Simpi a écrit:pour les stabilités j'ai du mal à les etablir

Tu considère une famille
_{j \in J})
d'ouverts de
)
et tu partage l'ensemble

en deux :
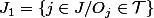
et
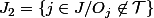
. Tu remarques ensuite que:
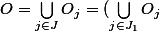 \cup (\bigcup_{j \in J_2} O_j))
.
Si tu analyses attentivement les deux termes de cette union, tu arrivera à des bonnes fins, surtout si tu utilises des propriétés relatives à l'intersection d'une famille quelconque de fermés et la nature d'un fermé contenu dans un compact.
Note: Vu que tu en aura besoin par la suite, tu peux essayer d'abord, dans un premier temps, de prouver que si

et

un compact de
)
alors
 \in \mathcal{T}')
.

C'est la même démarche pour la stabilité par intersection finie (tu pourra te contenter de deux ouverts).
car
qui appartient à