Les équations algebriques enfin résolues

[manoa]

genre les 22 d'avant ont échoué

:ptdr: :ptdr:

ça serait sympa d'avoir un résultat marocain, je t'encourage barbu ! :zen:

[Dinozzo13]

en tout cas je trouverais marrant de voir dans les copies
D'après le corollaire du barbu23, nous avons .... :ptdr:

genre les 22 d'avant ont échoué

J'adore c'te réflexion :++: : "D'après le théorème de barbu23"

[Kikoo <3 Bieber]

J'ai qu'une seule chose à dire : Allez barbu23 !!! On est tous derrière toi !!!! :D

[barbu23]

Merci à vous tous. :happy3:
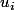
@leon : les sont dans .
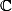
Mes travaux ne s'appuient sur aucune référence bibliographique, parce que ça ne demande pas beaucoup d'efforts. si tu sais appliquer la méthode aux équations de second degré, tu sauras la résoudre pour le degré , , , ... etc, parce que tu appliques la même méthode. :happy3:

[leon1789]

si tu sais appliquer la méthode aux équations de second degré, tu sauras la résoudre pour le degré , , , ... etc, parce que tu appliques la même méthode.

Les degrés 3, 4, 5, se traitent comme le second degré... C'est pas clair ce que tu dis.


1) Peux-tu nous présenter les solutions de x^3-x+1=0 et de x^4-x+1=0 ?


2) Peux-tu nous présenter les solutions de x^5-x+1=0 ? de x^6-x+1=0 ? de x^7-x+1=0 ? l'un des trois exemple suffira.

[barbu23]

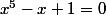
Attend @leon, je viendrai te donner la factorisation de : dans quelques heures ... C'est un peu long le calcul. :happy3:
Cordialement. :happy3:

[barbu23]

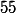
Non, je préfère donner la méthode au lieu de faire des calculs ennuyeux et trop long sans grand intérêt ... Il y'a aucun gout la dedans, ça m’énerve ... :mur: Il faut calculer l'inverse de deux matrices , et tu as le choix de poser n'importe quoi la dedans dans ces matrices suivant une règle bien sûr ... le calcul est trop exténuant ... je ne peux pas ... Est ce que je peux publier ma méthode sur arxiv.org, et comment ? désolé @ léon ... je suis incapable de faire le calcul ... :triste:

[leon1789]

La lourdeur des calculs n'est pas étonnante : une célèbre citation de Galois, « en un mot les calculs sont impraticables ».
Mais je pensais que tu pourrais utiliser une machine...

Quelles sont tes matrices 5x5 ? Je vais les inverser en utilisant un logiciel.

Et sur l'exemple le plus simple : ?

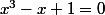
[alm]

Salut :

Et sur l'exemple le plus simple : ?

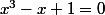
Oui c'est vrai! le mieux est de montrer ce qui se passe à travers un exemple simple.
Pour éviter les cas connus donnons un exemple de degré .
On demande à barbu 23 si sa méthode peut nous donner explicitement les racines réelles et non réelles complexes de l'équation :
(Cette équation admet une racine réelle rationnelle).


PS : à barbu23
- Tes jugements à propos des profs marocains ne sont pas fondés. Tu dis que tu ne connaît personne et puis tu dis: ' il n'y'a personne pour t'écouter et prendre de son temps pour t'aider ... '
- Pourquoi tu veux que le monde connaisse ce que tu as fait ? Si nécessaire est ça doit venir au dernier moment. non ? A ce moment tu dois d'abord t'assurer de la vérité des étappes de tes raisonnements, les discuter et les expliquer, ensuite si ces travaux ont un interrêt attirant ce sont les gens qui vont te demander de leur en parler davantage et pas le contraire.

Amicalement
Mohamed.

[barbu23]

Je veux que tous le monde connaisse ce que j'ai fait, c'est vrai, mais c'est juste pour que dans les prochaines siècles qui viennent ( Inchallah ), et bien les gens qui lisent ce genre d'articles savent que c'est moi "Omar" qui a trouvé la résolution à ce genre d'équations et non quelqu'un d'autres ... :zen:
Pour le moment, je ne suis pas prêt pour faire de long calculs inutils, et je crains que vous me prenez pour un con, parce que, parce que vous allez avoir des chiffres comme ça : , , et vous allez dire, mais il se moque de nous ce mec ou quoi ? :ptdr: D'où vient tous ce calcul ? ET bien simplement parce que, comme je vous ai dit, on a le choix de mettre n'importe quel chiffre dans la matrice, l'essentiel, c'est de respecter une règle ( une formule ) ...

[fatal_error]

Bon c'est pas la peine de venir radoter "j'ai la formule, mais jvous la donne pas et jvous montre pas qu'elle marche". Ca fait même pas baver puisque si tu montres pas qu'elle marche par défaut c'est que ca marche pas. Tout ce que ca fait c'est faire supposer que c'est dla chiasse qui est pas testée.

Alors je demande qu'à me tromper mais bon, ca va on a compris que tu as l'uber formule. Maintenant si t'arrives pas à trouver comment la rendre dispo au grand publique, bon ... il te reste une dizaine d'années en rab. :lol3:

[barbu23]

@fatal-error :
Tu veux la voir, d'accord , mais, tu me dis d'abord comment la publier sur arxiv.org .. Quelqu'un m'a dit qu'il faut un compte d'abord, mais on ne donne pas un compte à n'importe qui ... il faut que tu sois membre de "je ne sais pas quoi" : étudiant à l'université qui s'occupe de ce web site ... je ne le suis pas malheureusement ...
@MOHAMED :
C'est pour l'histoire, pour qu'elle soit témoin de mes travaux et pour que les prochaines générations savent que c'est moi le père de ces formules ... :zen:

[gdlrdc]

Tu n'as pas de calculatrice ou de logiciel qui inverse les matrices 5*5?
tu peux télécharger matlab.

[alm]

Salut:

C'est pour l'histoire, pour qu'elle soit témoin de mes travaux et pour que les prochaines générations savent que c'est moi le père de ces formules ... :zen:

OK, mais pour acceder à l'histoire il faut choisir les bonnes portes...je te laisse le soin de le chercher.
Pour arXiv on te dit qu'il suffit de poster ton message sur un ordinateur d'une faculté ... ce n'est pas dificile à réaliser.


Est ce que ta méthode peut nous donner explicitement toutes les racines de l'équation que j'ai proposé en haut ?

[Elerinna]

C'est pour l'histoire, pour qu'elle soit témoin de mes travaux et pour que les prochaines générations savent que c'est moi le père de ces formules ... :zen:

La paternité a été reconnue puisque la donnée s'est reproduite en essaimage sur futura-sciences...

Enfin, comme tout enquêteur de choc, prends garde à l'espion qui vient du froid dans la cour arrière.
L'espion peut aimer au secret les inventions en se révèlant une précieuse aide de taille au demeurant.
Lis la presse experte d'ici ou de l'étranger, tel le mémorial de mathématiques où ces 77 pages, dudit
Giuseppe Belardinelli peuvent être d'un accord parfait 50 ans plus tôt : le génie de la cave vit au frais.

[Joker62]

Moi j'ai prouvé l'hypothèse de Riemann, mais j'la garde pour moi :p

[barbu23]

@Elerinna :
Peux tu résumer ce qui est écrit sur ton lien : mémorial de mathématiques, parce que c'est long à lire.
Merci d'avance. :happy3:

[barbu23]

@Elerinna :
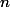
J'ai lu la petite introduction de ton mémorial, et il s'avère que les équations algébriques polynomiales ont dèjà des méthodes de résolution : Il est dit dans ce mémorial, que Betti et Lindemann donnèrent la résolution des équations de degré par des fonctions transcendantes liées aux fonctions hyperelliptiques.
Est ce que vous connaissez en détail cette méthode ?
Merci d'avance. :happy3:

[acoustica]

Moi j'ai prouvé l'hypothèse de Riemann, mais j'la garde pour moi :p

Ca me rappelle le top-niveau fil qu'on avait eu il y a quelques années sur la 50 762 ème démonstration de la conjecture de Syracuse. La démonstration était à-peu-près celle-ci : "regardez, il y a des symétries partout, c'est évident". :ptdr:

[leon1789]

Tu veux la voir, d'accord , mais, tu me dis d'abord comment la publier sur arxiv.org ..

Décidément, tu ne comprends pas comment fonctionnent les choses : traite d'abord un exemple parmi tous ceux qui ont été proposés !

Au départ c'était marrant, mais là tu t'enfonces... c'est bien dommage.

..et en plus, tu as fait exactement le même topo sur futura-sciences... :mur: