Les équations algebriques enfin résolues
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 19 Mai 2012, 10:32
par barbu23 » 19 Mai 2012, 10:32
leon1789 a écrit:pourquoi a-t-on

?
Parce qu'on peut toujours trouver

dans

tel que
 = a $)
quant

, non ? corrige moi si je dis n'importe quoi, j'ai arrêté les études il y'a longtemps. :happy"/

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 19 Mai 2012, 10:33
par leon1789 » 19 Mai 2012, 10:33
barbu23 a écrit:Parce qu'on peut toujours trouver

dans

tel que
 = a $)
quant

, non ?
comment as-tu défini
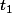
et
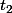
? leur définition ne vient pas de
 = cste)
, donc ta réponse n'est pas valable.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 19 Mai 2012, 10:35
par barbu23 » 19 Mai 2012, 10:35
leon1789 a écrit:comment as-tu défini
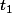
et
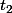
? leur définition ne vient pas de cos(t1-t_2) = cste, donc ta réponse n'est pas valable.
Les

et

sont arbitraire. :happy3:

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 19 Mai 2012, 10:38
par leon1789 » 19 Mai 2012, 10:38
barbu23 a écrit:Les

et

sont arbitraire. :happy3:
ils sont arbitraires !? :ptdr: Mais c'est toi qui pose leur définition quelque part, relis ton texte.
Encore une réponse non valable...
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 19 Mai 2012, 10:44
par barbu23 » 19 Mai 2012, 10:44
leon1789 a écrit:ils sont arbitraires !? :ptdr: Mais c'est toi qui pose leur définition quelque part, relis ton texte.
Encore une réponse non valable...
Non on ne s'entend pas bien là, j'ai posé
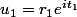
, et
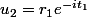
, donc :
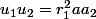
, donc, là,

n'intervient pas, il est arbitraire ... la même chose pour

... quant est ce qu'il ne devient pas arbitraire ? c'est quant on s'aprête pour résoudre l'équation :
 = a_1 $)
... tu comprends maintenant ?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 19 Mai 2012, 10:50
par leon1789 » 19 Mai 2012, 10:50
barbu23 a écrit:Non on ne s'entend pas bien là, j'ai posé
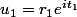
, et
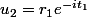
r_1 et t_1 sont-ils des réels ? Tout laisse à croire que oui, mais comme tu ne dis rien à ce sujet, c'est flou.
Si effectivement, ils sont réels, alors comment montres-tu u_1 et u_2 sont conjugués ?
Même questions pour r_2 et t_2, v_1 et v_2.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 19 Mai 2012, 10:51
par barbu23 » 19 Mai 2012, 10:51
leon1789 a écrit:r_1 et t_1 sont-ils des réels ? Tout laisse à croire que oui, mais comme tu ne dis rien à ce sujet, c'est flou.
Pas forcément, seuls les
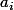
sont dans

.
Les

sont dans

quant les

.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 19 Mai 2012, 10:54
par leon1789 » 19 Mai 2012, 10:54
barbu23 a écrit:Pas forcément, seuls les
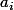
sont dans

.
Ok, donc les r_i, u_i, v_i, t_i sont complexes.
Dans ce cas, comment définis-tu cos(t_1-t_2) ? et aussi arccos d'une constante complexe ?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 19 Mai 2012, 10:55
par leon1789 » 19 Mai 2012, 10:55
Ok, donc les r_i, u_i, v_i, t_i sont complexes en général.
Dans ce cas, comment définis-tu cos(t_1-t_2) ?
... et aussi arccos d'une constante complexe ?

-
alm
- Membre Relatif
- Messages: 335
- Enregistré le: 15 Jan 2009, 01:00
- Localisation: Salé, Maroc
-
 par alm » 19 Mai 2012, 10:55
par alm » 19 Mai 2012, 10:55
Salut ,
à barbu23:
Encore une preuve que tu a fait beaucoup de besogne:
si
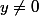
,
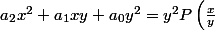)
où
=a_2X^2+a_1 X +a_0)
On factorise

dans

;
=a_2(X-u)(X-v))
Alors en posant
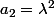
,
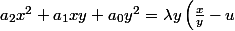 \lambda y \left(\frac xy -v \right) = (\lambda x - \lambda uy)(\lambda x - \lambda v y))
, valable aussi si

PS; Si tu veux généraliser, le mot c'est : polynômes homogènes ....
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 19 Mai 2012, 10:57
par barbu23 » 19 Mai 2012, 10:57
leon1789 a écrit:Ok, donc les r_i, u_i, v_i, t_i sont complexes en général.
Dans ce cas, comment définis-tu cos(t_1-t_2) ?
... et aussi arccos d'une constante complexe ?
Il est définit tel que :
 = a_1 $)
On, traite deux cas :
-

-


-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 19 Mai 2012, 11:05
par leon1789 » 19 Mai 2012, 11:05
barbu23 a écrit:On le définit tel que :
 = a_1 $)
On, traite deux cas :
-

-

qu'est ce que cela veut dire ? t_1 et t_2 sont déjà fixés.
En plus la constante (qui n'est pas a_1) est complexe...
je répète ma question : comment définis-tu la fonction cosinus sur C ? et la fonction arccos sur C ?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 19 Mai 2012, 11:11
par barbu23 » 19 Mai 2012, 11:11
leon1789 a écrit:qu'est ce que cela veut dire ? dis-moi ce comment tu définis la fonction cosinus sur C ? et la fonction arccos sur C ?
ça veut dire que dans les deux cas, il existe

tel que :
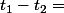
avec :
 = a_1 $)
(

solution de l'équation
 = a_1 $)
) tel que
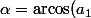 $)
( tu choisis la détérmination de la fonction

qui convient ).
Dans, ce cas, on peut écrire :
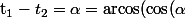 ) $)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 19 Mai 2012, 11:12
par barbu23 » 19 Mai 2012, 11:12
MOHAMED_AIT_LH a écrit:Salut ,
à barbu23:
Encore une preuve que tu a fait beaucoup de besogne:
si
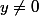
,
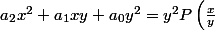)
où
=a_2X^2+a_1 X +a_0)
On factorise

dans

;
=a_2(X-u)(X-v))
Alors en posant
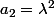
,
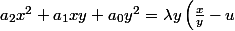 \lambda y \left(\frac xy -v \right) = (\lambda x - \lambda uy)(\lambda x - \lambda v y))
, valable aussi si

PS; Si tu veux généraliser, le mot c'est : polynômes homogènes ....
C'est pas ça, ce qu'on cherche. :happy3:

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 19 Mai 2012, 11:15
par leon1789 » 19 Mai 2012, 11:15
barbu23 a écrit:ça veut dire que dans les deux cas, il existe

tel que :
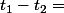
et
 = a_1 $)
et
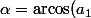 $)
Dans, ce cas, on peut écrire :
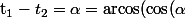 ) $)
Tu utilises allègrement des fonctions cos et arccos avec des nombres complexes.. Mais sont-elles définies sur C ? comment ?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 19 Mai 2012, 11:22
par barbu23 » 19 Mai 2012, 11:22
leon1789 a écrit:Tu utilises allègrement des fonctions cos et arccos : sont-elles définies sur C ? comment ?

et donc

car
 = a_1 $)
et

... J'ai dit : il existe

, ça veut dire que tu choisis la "determination" de la fonction

qui convient. :happy3:
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 19 Mai 2012, 11:25
par Joker62 » 19 Mai 2012, 11:25
ça devient ridicule là Barbu.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 19 Mai 2012, 11:29
par barbu23 » 19 Mai 2012, 11:29
Joker62 a écrit:ça devient ridicule là Barbu.
C'est pas de cette manière qu'on fait une critique. tu ajoutes rien de bien fondé à la discussion.

-
alm
- Membre Relatif
- Messages: 335
- Enregistré le: 15 Jan 2009, 01:00
- Localisation: Salé, Maroc
-
 par alm » 19 Mai 2012, 11:34
par alm » 19 Mai 2012, 11:34
barbu23 a écrit:C'est pas ça, ce qu'on cherche. :happy3:
tu cherchais à afctoriser

. Non ?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 19 Mai 2012, 11:36
par barbu23 » 19 Mai 2012, 11:36
J'ai commis un abus de langage, j'aurai pu noter
 $)
au lieu de
 $)
, c'est général, car c'est une détermination de la fonction

... Donc, au lieu d'écrire
 ) $)
, j'écris
 ) $)
avec

la détermination de l'inverse de la fonction

sur une domaine simplement connexe.
C'est normal de faire des erreurs, ça fait des années que j'ai quitté la fac. :happy3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
?
, et