Salut
En plus, tu dis que c'est une nouvelle méthode! Or c'est une besogne par rapport à ce qu'un chercheur doit connaître.
En effet , à voir l'expression :
=ax^2+2bxy+cy^2)
avec

des nombres réels, tu peux dire que :
={^tX}AX)
où
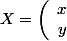)
et
)
.
La matrice

étant réelle symetrique , elle est diagonalisable :
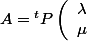 P)
où

est une matrice orthogonale.
Il vient :
={^tX}^tPDPX = {^tY}DY)
où
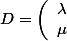)
et
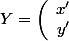 = PX)
.
Ainsi
=\lambda x'^2 + \mu y'^2 = (\alpha x')^2 - (\beta y')^2)
où
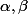
sont des nombres complexes tels que
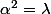
et
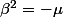
.
Donc :
=(\alpha x' + \beta y')(\alpha x' - \beta y'))
En tenant compte de fait que
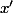
et
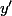
sont des expressions linéaires de

et

, on arrive à ce que tu desirais démontrer.
PS: Je précise que pour un vrai chercheur les détails ci-dessus sont encore superflus car le résultat est tellement connu que ce que tu appelles nouveau est une évidence.
Je t'avais dit d'accéder à l'histoire (puisque tu le veux) par les bonnes portes.
Je pense que la première de ces portes est d'éliminer cette précépitation de vouloir arriver à une réalisation tel que les gens ayant déjà franchi des pas dans la recherche n'y pensent même pas ... et remplacer cette précipitation par une volonté sincére de commencer par le commencement.
Les profs sont et doivent être méchants quand il s'agit d'étudiant à qui tu demandes de lire un article et te réponds : 'ça m'énérve de le lire '.
Si tu ne passes pas par cette étape qui necessite une vraie patience tu n'es certainement pas dans la bonne voie.
Cordialement et amicalement
Mohamed.
