Rebonjour,
On considere:
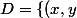\in R^2, x^2+y^2 \le 1 \})
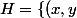\in R^2, xy \ge 0 \})
et
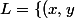\in R^2, \left| x \right| \le y \le x^2 \})
1)Determiner si

,

et

sont ouverts, fermé, compact, connexe
2) Meme question pour

,

, et

3) Indiquer le nombre de composantes connexes de

, de

, de

, et de
)
.
Mes elements de reponses:
1) les compacts, ouverts et fermé là ca va.
Mon probleme se trouve au niveau des connexes.
d'apres la definition on dit qu'une partie

de

est connexe si elle n'admet pas de partition en deux ouverts ou deux fermé. Donc si j'arrive à montrer qu'une partie admet une partition en deux ouverts ou en deux fermés alors la partie n'est pas connexe.
si je prend le

je pose alors
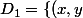\in R^2, -1\le x \le 0 et -1\le y \le 0 \})
et
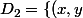\in R^2, 0 < x \le 1 et 0 < y \le 1 \})
on a

et
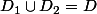
donc

et
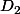
forme une partition de

donc

n'est pas connexe. Est ce que je suis la bonne voie?
