Les complexes

[philoux]

Bonjour à tous,

Je suis entrain de faire des révisions sur les nb complexes et j'ai un petit problème sur un exercice :

Voilà l'énoncé du problème:
Déterminer tous les nb complexes z qui vérifie : z* = 1/z

z* correspond au conjugé de z.

voici mon raisonnement :

z*z = 1 on sait que (z*z)^(1/2) = |z| -->

(z*z)^(1/2) = 1^(1/2)

donc j'obtiens le module du z = 1, ce que je ne comprend pas c'est comment égaler la formule de départ.
Merci à tous pour vos explications et vos suggestion.

Bonne année 2007 à tous !!! :briques:

A+ Philippe

[philoux]

Hello,

Merci pour ta réponse.

Mais je ne comprend pas comment tu obtiens z* = 1/r* exp(-iT), je ne comprend pas le 1/r. :mur:

car si z = a + bj --> r = (a^2+b^2)^(1/2)
T = arctg (b/a)
z = r exp(jT)

et z* = a - bj --> r = (a^2+b^2)^(1/2)
T = arctg (-b/a)
z = r exp(-jT)

Peut tu m'expliquer comment tu obtiens le "1/r", après ce sera claire pour moi.

Encore merci pour ta réponse !!!

A+
Philippe

[flight]

tout les nombres complexes de module 1 conviennent !

[yos]

Il y a des égarements alors j'écris tout :

[philoux]

Hello à tous !!!

Merci pour vos réponses.

Cette fois j'ai compris !!!

A+ Philippe

[philoux]

J'ai un autre pronlème à vous soumettre.

Voici le problème: dans un plan complexe, à quelle opération géométrique la multiplication par 1 + j correspond-t-elle ?

Voici mon raisonnement:

Je prends z = a + bj

z * (1 + j) = (a + bj) * (1 + j) = a-b + j(a+b)

j'ai pris par exemple a = 3 et b = 2 pour z

pour z * (1 + j) = (3 + 2j) * (1 + j) = 1 + j5

le problème, c'est que je n'arrive pas a voir une correspondance géométrique entre z et z * (1 + j).
J'ai même essayé de passer en exp ce qui me donne pour z = (13)^(1/2)exp(2/3)
et pour l'autre z * (1 + j) = (24)^(1/2)exp(5)

Mais c'est la meme chose, je ne vois pas :marteau:

Merci d'avance pour vos futurs suggestions

Philippe

[yos]

1+j=, donc on tourne de autour de O.

[philoux]

Merci pour la réponse,

en fait la multplication de (1 + j) pour un nombre complexe quelconque = z * 2^(1/2) exp(pi/4) ce qui revient à faire par rapport à l'angle initial + pi/4.

Merci pour ton explication.

A bientot

Philippe

[yos]

Mais tu ne m'as pas lu!! J'ai jamais parlé de 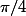. Pour moi, j est le complexe de module 1 et d'argument 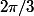. Maintenant si tu confonds i et j, c'est autre chose. et tu as le fait suivant :

Multiplier par , correspond à deux opérations géométriques successives et dans l'ordre qu'on veut :
1) la rotation de centre O, d'angle t,
2) l'homothétie de centre O de rapport r.
La succession de ces deux transformations porte le nom de similitude directe de centre O, d'angle t et de rapport r.

[philoux]

Merci pour ta réponse Yos,

Excuse moi, mais comme cela se voit peut-être, je ne suis pas un doué en math, mais je m'accroche :++:.

Je veux juste apporté une précision, dans l'école ou je suis, lors du traitement de nb complexes, on remplace le i par le j, car en électronique le i est utilisé pour des courants, ce qui évitent lors de calculs avec les nb complexes de se tromper. Je fais des études en électronique. Fin de la remarque!

Voilà maintenant, je passe à mon nouveau problème, celui-ci se partage en 2 question :

H = jwL/(R+jwL)

1) convertir H sous forme exponentielle:

ce qui me donne H =

2) c'est à la 2ème question que je pêche

Calculer la limite de (arg(H)) quand w --> +infini

l'argument de H pour moit est:

donc ce que j'obtiens c'est lim quand w --> + infini
ce qui me donne -arctg(+infini), mais je ne sais pas comment convertir ce chiffre, maintenant. J'ai vu à la machine que arctg(infini) donnait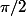 , mais je ne comprend pas pourquoi ??

Est-ce que quelqu'un peu m'aider, voir m'expliquer pourquoi ce résultat. Est-ce que je suis sur la bonne voie sur le raisonnement que je fais.

Merci et A+ Philippe

[yos]

J'avais compris que j'avais affaire à un physicien. Personne n'est parfait.
.
C'est parce que .