Lemmes de Jordan

[silent_james]

Bonsoir à tous,

J'ai un léger problème sur une application des lemmes de Jordan.

On se donne une fonction f de C dans C holomorphe pour R assez grand.
On veut montrer que son intégrale sur un arc de cercle de centre l'origine tend vers 0 quand R (le rayon de l'arc) tend vers l'infini.

Le corrigé donne (pr une certaine fonction f que je ne précise pas) :
on a z*f(z) tend vers 0 quand |z| tend vers l'infini
ce qui implique R*M(R) tend vers 0 quand R tend vers l'infini (où M(R) est le sup de |f| sur l'arc de cercle).
J'ai du mal à voir facilement cette implication bien qu'elle ait été écrite de manière évidente.

Voilà ce que j'ai fait :
z*f(z) tend vers 0 quand |z| tend vers l'infini
<=> | z*f(z)| tend vers 0 quand |z| tend vers l'infini
Centre = origine donc |z| = R
f(z) = f(R, têta)
on a :
R*|f(R, têta)| tend vers 0 simplement qd R tend vers l'infini pour tout têta appartenant à [têta0, têta1]
donc
R*|f(R, têta)| tend vers 0 presque uniformément qd R tend vers l'infini.
Ce qui me contrarie, c'est le "presque" !

Donc je suis bloqué....
J'aimerais savoir si ce que j'ai fait est correct et seulement incomplet ou alors si quelque chose d'évident me passe au dessus de la tête.

Voilà,
Je vous remercie par avance

[tize]

Bonjour,
contraposée :
par compacité de l'arc et continuité de f il existe dans l'arc tel que et si ne tend pas vers 0 alors non plus...

[silent_james]

ok !
Je te remercie sincèrement tize !
Sinon tu penses qu'en partant comme je l'ai fait, on aurait pu conclure ?

[tize]

Là où il y a un problème c'est quand tu écris :
"R*|f(R, têta)| tend vers 0 simplement..."
en fait R*|f(R, theta)| tend vers 0 indépendamment de theta et même pour un theta_R ou f prendrait son sup...
Pour résumer : R*|f(R, theta)| tend vers 0 indépendamment de theta ce n'est pas la même chose que : "à theta fixé R*|f(R, theta)| tend vers 0" (ça c'est la convergence simple)

[silent_james]

Mais pourtant, par hypothèse on a z*f(z) tend vers 0 qd |z| -> infini
ce qui implique à mon avis : à têta fixé, R*|f(R, têta)| tend vers 0 qd R -> infini

Mon problème était justement le fait que la convergence n'était pas uniforme.
(c'est pourquoi j'ai utilisé Egoroff pr montrer la convergence presque uniforme)
D'apres ce que tu me dis,
( "z*f(z) tend vers 0 qd |z| -> infini" ) => R*f(R, têta) converge uniformément vers 0 qd R -> infini et dans ce cas, le problème de savoir si le sup est atteint ou non n'a pas d'importance.


Si tu peux m'éclairer...

[tize]

Salut,
pourquoi serait-ce à theta fixé, quand on dit :
" quand |z| tend vers l'infini " cela veut dire (comme tu l'as écrit) quand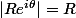 tend vers l'infini mais il ne faut pas oublier que c'est quand même qui varie dans C de manière à ce que son module tend vers l'infini; et pendant que 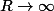theta fait ce qu'il veut lui...

[silent_james]

Salut Tize !

En fait, j'avais fait l'analogie dans le cas d'une famille dénombrable :
soit f(x)_n une famille de fonctions telle que f(x)_n tend vers 0 quand n tend vers l'infini, dans ce cas, comme je l'ai toujours vu, la convergence est simple.
J'ai appliqué ça pour R = n et têta = x.

-Le truc, c'est que ça me paraissait juste ? (je m'accroche lol)

-Ensuite, si c'est indépendant de têta, ça marche aussi pour le sup, et donc on conclut sans utiliser le fait que f atteint ses bornes ?

En tout cas, je te remercie de prêter attention à mon problème !

[tize]

De rien :we:

[silent_james]

... :mur:

[silent_james]

Est-ce que quelqu'un aurait la solution s'il vous plaît...
Parce que, c'est pas très clair pour moi...

[silent_james]

Personne ne peut m'éclairer ?
:help: :help:

[silent_james]

Bon, personne ne répond, donc soit personne ne sait, soit personne ne juge utile de m'aider car tout a été dit... mais si vous voyez une énorme absurdité dans mon dernier post où fait l'analogie dans le cas d'une famille dénombrable... alors dites le moi !!