Lemme de Lebesgue

[exilim]

Bonjour!
Je suis a la recherche d'un peu d'aide pour démontrer le lemme de Lebesgue :
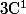
soit g une fonction de classe sur le segment [a,b] ( avec a < b )
alors
Comment prouver ce résultat?
merci de votre aide!

[Ju.]

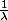
Juste une petite idée : a tu pensé a faire une intégration par parties ainsi tu fait apparaitre un utile pour le passage à la limite.
Utilise aussi le fait que la dérivée de g est bornée pour majorer la valeur absolu de g' cos(lambda t)

[kazeriahm]

le lemme de lebesgue est vrai de manière plus générale pour g de classe C0, ici oui comme g est C1 on integre par partie, il sort un 1/lambda qui ramene tout se beau monde a 0

[tize]

Il me semble que ce lemme est même vrai pour toutes fonctions intégrables (par densité)